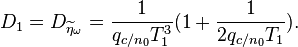Дискриминатор частоты оптимальный при малом отношении сигнал/шум — различия между версиями

Материал из SRNS
Перейти к: навигация, поиск
(→‎Особенности работы)
(→‎Сравнение с другими ЧД)
 
(не показаны 16 промежуточных версий 1 участника)
Строка 1: Строка 1:
 
{{Заготовка}}
 
{{Заготовка}}
−
 
+
{{TOCright}}
−
=Описание дискриминатора=
+
 
Дискриминатор описывается выражением <br />
 
Дискриминатор описывается выражением <br />
  
Строка 11: Строка 10:
 
<math>I'_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = -\sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)(l-1)T_d\mbox{sin}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))</math>,<br />
 
<math>I'_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = -\sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)(l-1)T_d\mbox{sin}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))</math>,<br />
 
<math>Q'_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)(l-1)T_d\mbox{cos}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))</math>,<br />
 
<math>Q'_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)(l-1)T_d\mbox{cos}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))</math>,<br />
 +
<math>L=\frac{T}{{{T}_{d}}}</math> - число отсчетов за время <math>T</math> интегрирования в корреляторе, <math>T_d</math> - интервал дискретизации.
  
 
== Особенности работы ==
 
== Особенности работы ==
−
Для работы дискриминатора требуется формирование особенных квадратур <math>I'_k, Q'_k</math>. Они представляют собой обычные квадратуры, умноженные на линейно-возрастающую функцию <math>(l-1)T_d</math> (индекс времени <math>l</math> растет - множитель растет).
+
Для работы дискриминатора требуется формирование особенных квадратур <math>I'_k, Q'_k</math>. Они представляют собой обычные квадратуры, умноженные на линейно-возрастающую функцию <math>(l-1)T_d</math> (индекс времени <math>l</math> растет - множитель растет). Аппаратно такой коррелятор не реализован. Есть предложение <ref name="KorPhD">[[Публикация:Корогодин 2013 Разработка алгоритмов обработки сигналов СНС в аппаратуре определения угловой ориентации объектов]]</ref> заменить честный расчет <math>I'_k, Q'_k</math> суммой взвешенных корреляционных сумм: <br />
 +
 
 +
<math>I'_{k}\left( {{{\tilde{\tau }}}_{k}},{{{\tilde{\omega }}}_{{{d}^{{}}}k}} \right)\approx -{{T}_{small}}\sum\limits_{n_{1}^{{}}=1}^{N_{1}^{{}}}{n_{1}^{{}}{{Q}_{{{n}_{1}},k}}},</math><br />
 +
<math>
 +
Q'_{k}\left( {{{\tilde{\tau }}}_{k}},{{{\tilde{\omega }}}_{{{d}^{{}}}k}} \right)\approx {{T}_{small}}\sum\limits_{n_{1}^{{}}=1}^{N_{1}^{{}}}{n_{1}^{{}}{{I}_{{{n}_{1}},k}}}.</math>
 +
 
 +
По этой методике весь интервал интегрирования в корреляторе разбивается на <math>N_1</math> равных частей длительностью <math>T_{small}</math>. На этих малых интервалах рассчитываются традиционные корреляционные суммы <math>I_{n_1, k}, Q_{n_1, k}</math>, а потом проводится их взвешенное суммирование. Чем больше <math>N_1</math>, тем точнее оказывается приведенная методика. Допустим "большой" коррелятор копит <math>T = 10</math> мс, тогда целесообразно выбрать <math>T_{small} = 1</math> мс и <math>N_1 = 10</math>.
  
 
== Дискриминационная характеристика ==
 
== Дискриминационная характеристика ==
  
−
Сделано допущение, что <math>\varepsilon_{\omega,k-1} = \varepsilon_{\omega,k}</math>.
+
Дискриминационная характеристика <ref name="KorPhD">[[Публикация:Корогодин 2013 Разработка алгоритмов обработки сигналов СНС в аппаратуре определения угловой ориентации объектов]]</ref>:
  
−
<math>U(\varepsilon_\omega) = A_{IQ}^2\rho(\varepsilon_{\tau,k})\rho(\varepsilon_{\tau,k-1})\mbox{sinc}^2(\varepsilon_{\omega,k-1}T/2)\mbox{sin}(\varepsilon_{\omega,k-1}T),</math>
 
  
−
где <math>A_{IQ} = \frac{AL}{2}</math>, <math>A</math> - амплитуда сигнала <math>y(t_{k,l})</math>, <math>L</math> - количество отчетов, накапливаемых в корреляторе, <math>\varepsilon</math> - разность истинного и опорного параметров.
+
<math>U\left( \delta \omega  \right)=A_{IQ}^{2}T\frac{\text{sinc}\left( \frac{\delta \omega T}{2} \right)}{\delta \omega T}\left( \text{sinc}\left( \frac{\delta \omega T}{2} \right)-\cos \left( \frac{\delta \omega T}{2} \right) \right)</math>,
  
−
Крутизна дискриминационной характеристики при нулевой расстройке по частоте: <math>S_D = A_{IQ}^2T</math>.
+
где <math>A_{IQ} = \frac{AL}{2}</math>, <math>A</math> - амплитуда сигнала <math>y(t_{k,l})</math>, <math>L</math> - количество отчетов, накапливаемых в корреляторе, <math>\delta\omega</math> - разность истинного и опорного параметров.
  
−
В модели задержка сигнала полагалась известной: <math>\rho(\varepsilon_{\tau,k}), \rho(\varepsilon_{\tau,k-1}) = 1</math>.
 
  
−
Дискриминационная характеристика при различных временах накопления:
+
Крутизна при нулевой ошибке по частоте <ref name="KorPhD">[[Публикация:Корогодин 2013 Разработка алгоритмов обработки сигналов СНС в аппаратуре определения угловой ориентации объектов]]</ref>:
−
<center><gallery mode="packed" widths="400px" heights="400px">
+
−
Файл:20151028_DhChd_new.png|Дискриминационная характеристика при T=1 мс
+
−
Файл:20151028_DhChd_newT5ms.png|Дискриминационная характеристика при T=5 мс
+
−
</gallery></center>
+
  
−
== Флуктуационная характеристика ==
+
<math>S_D=\frac{1}{12}A_{IQ}^{2}{{T}^{2}}</math>
  
−
Получены зависимости СКО шума на выходе дискриминатора от <math>q_{c/n_0}</math> для различных времен накопления. Теоретические кривые пунктирной линией.
 
  
−
[[File:20132504 CKO(q,T) ChD.png|300x300px|frame|center|]] <br />
+
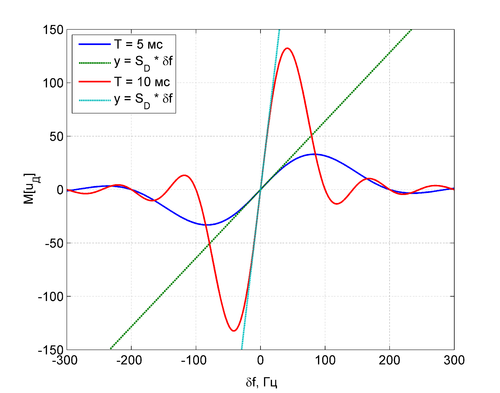
Вид дискриминационной характеристики для разных времен накопления и <math>q_{c/n0} = 50</math> дБГц:
  
−
Дисперсия шума эквивалентного наблюдения частоты, т.е. шума с выхода дискриминатора, пересчитанного '''к его входу''' при нулевой расстройке по частоте: <br />
+
[[File:20151103_FreqDiskr.png|центр|500px]]
  
−
<math>D_{\widetilde{\eta}_\omega} = \frac{1}{q_{c/n_0}T^3}(1+\frac{1}{2q_{c/n_0}T}).</math>
+
== Флуктуационная характеристика ==
 +
Дисперсия шума эквивалентного наблюдения частоты, т.е. шума с выхода дискриминатора, пересчитанного '''к его входу''' при нулевой расстройке по частоте <ref name="OptimalFLL">[[Публикация:Корогодин 2013 Потенциальные характеристики оценивания частоты в некогерентном приемнике]]</ref>: <br />
  
 +
<math>D_{\widetilde{\eta}_\omega} = \frac{6}{q_{c/n_0}T^3}(1+\frac{1}{q_{c/n_0}T}).</math>
  
−
Интересно сравнить дисперсию шумов по входу для разных дискриминаторов. На данный момент у нас есть:
+
=== Сравнение с другими ЧД ===
−
* Собственно дисперсия шума на входе рассматриваемого в этой статье дискриминатора. Обозначим ее как <math>D_1</math>:  
+
Интересно сравнить дисперсию шумов по входу для различных дискриминаторов:
  
−
<math> D_1 = D_{\widetilde{\eta}_\omega} = \frac{1}{q_{c/n_0}T_1^3}(1+\frac{1}{2q_{c/n_0}T_1}).</math>
+
* Дисперсия шума на входе [[Дискриминатор частоты с временным сдвигом квадратурных компонент|дискриминатора с временным сдвигом квадратурных компонент ("cross")]]. Обозначим ее как <math>D_1</math>:
  
−
* Дисперсия шума на входе оптимального при низком отношении сигнал/шум частотного дискриминатора (тот, который <math>I_kI'_k+Q_kQ'_k</math>). Формула из диссера Корогодина И. В., или, например, из этой [[Публикация:Корогодин 2013 Потенциальные характеристики оценивания частоты в некогерентном приемнике|статьи]]. Обозначим ее как <math>D_2</math>:
+
:<math> D_1 = D_{\widetilde{\eta}_\omega} = \frac{1}{q_{c/n_0}T_{1}^3}(1+\frac{1}{2q_{c/n_0}T_{1}}).</math>
  
−
<math> D_2 = D_{\widetilde{\eta}_\omega} = \frac{6}{q_{c/n_0}T_2^3}(1+\frac{1}{q_{c/n_0}T_2}).</math>
+
* Дисперсия шума на входе рассматриваемого в этой статье дискриминатора:
  
 +
:<math> D_2 = D_{\widetilde{\eta}_\omega} = \frac{6}{q_{c/n_0}T_{2}^3}(1+\frac{1}{q_{c/n_0}T_{2}}).</math>
  
−
Вообще говоря, время накопления в корреляторах может быть различно. Если принять равными времена <math>T_1</math> и <math>T_2</math>, получится что дискриминатору с временным сдвигом квадратур (c <math>D_1</math>) нужны будут квадратуры, накопленные на суммарном времени <math>2T_1</math> и разбитые по времени пополам. Для корректности сравнения положим, что во втором дискриминаторе (у которого <math>D_2</math>) коррелятор копит на времени <math>T_2 = 2T_1</math>. Разделим <math>D_2</math> на <math>D_1</math>. После нехитрых вычислений окажется, что
+
Пусть cross дискриминатор реализован [[Дискриминатор частоты с временным сдвигом квадратурных компонент#Особенности работы|по схеме без перекрытия]], тогда <math>T_{2} = 2T_{1}</math> и
  
−
<math>\frac{D_2}{D_1} = \frac{6}{8}</math>, т. е. <math>D_2 = 0.75*D_1</math> или для СКО:<math>\sigma_2 = 0.866*\sigma_1</math>.
+
:<math>\frac{D_2}{D_1} = \frac{6}{8}</math>,  
  
−
Таким образом, по дисперсии шумов наблюдается не очень то большая разница между сравниваемыми дискриминаторами. На рисунке ниже приведен график зависимости СКО эквивалентных шумов представленных ЧД от отношения сигнал/шум q_{c/n0}.
+
или для СКО:
 +
 
 +
:<math>\sigma_2 = 0.866*\sigma_1</math>.
 +
 
 +
Дискриминатор cross проигрывает <math>I_kI'_k+Q_kQ'_k</math> около 15% по СКО во всем диапазоне с/ш. На рисунке ниже приведен график зависимости СКО эквивалентных шумов представленных ЧД от отношения сигнал/шум <math>q_{c/n0}</math>
  
 
[[File:20151029_Сравнение СКО.png|центр|500px]]
 
[[File:20151029_Сравнение СКО.png|центр|500px]]
  
−
== Листинг модели ==
 
−
Ниже представлен листинг модели, с которой сняты картинки.
 
−
{{Hider
 
−
|title = Листинг модели
 
−
|content = <source lang = matlab>
 
−
clear all
 
−
clc
 
−
close all
 
  
−
plotDX = 1; %считаем ДХ
+
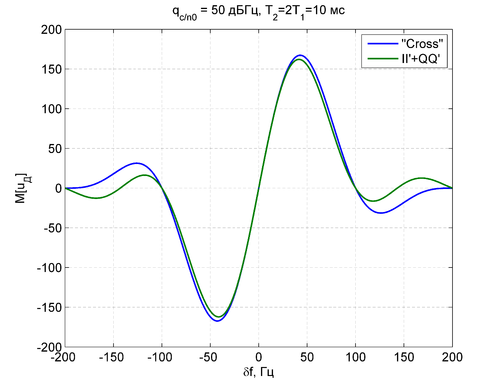
Далее построены нормированные на крутизну дискриминационные характеристики сравниваемых дискриминаторов. Как и при сравнении дисперсий шума, полагаем <math>T_2 = 2T_1</math>.
−
plotFX = 0; %считаем дисперсию шумов
+
  
−
if plotDX
+
[[File:20151103_FreqDiskrCompare.png|центр|500px]]
−
    N = 3000;
+
 
−
    stdn_IQ = 8;
+
 
−
    Tc = 0.005;
+
Из приведенного рисунка следует вывод, что апертура обоих частотных дискриминаторов равна <br />
−
    qcno_dB = 45;
+
<math>A_\omega=\frac{2}{T_u}</math>.<br />
−
    qcno = 10^(qcno_dB/10);
+
<math>T_u</math> - темп работы дискриминатора. Ранее дискриминаторы сравнивались при условии <math>T_u = T_2 = 2T_1</math>, т.е. при одинаковом темпе работы. При анализе "cross" дискриминатора нужно помнить, что <math>T_1</math> в формулах его характеристик - это время когерентного накопления в корреляторе, а темп работы самого дискриминатора по схеме без перекрытия <math>T_u = 2T_1</math>.
−
   
+
 
−
    wdop_real = 2*pi*100;
+
== Листинг модели ==
−
    wdop_oporn = [wdop_real-2*pi*(1/Tc):2*pi*(2/Tc)/500:wdop_real + 2*pi*(1/Tc)];
+
−
   
+
−
    UdFLL = zeros(1, length(wdop_oporn));
+
−
   
+
−
    A_IQ = stdn_IQ * sqrt(2 * qcno * Tc);
+
−
    Sd = A_IQ^2*Tc;
+
−
   
+
−
    for k = 1:N
+
−
        for j = 1:length(wdop_oporn)
+
−
            n_I_old = 1*stdn_IQ * randn(1,1);
+
−
            n_I = 1*stdn_IQ * randn(1,1);
+
−
            n_Q_old = 1*stdn_IQ * randn(1,1);
+
−
            n_Q = 1*stdn_IQ * randn(1,1);
+
−
           
+
−
            phi_real = [pi/3 pi/3 + Tc*wdop_real(1)];
+
−
            phi_oporn =[pi/4 pi/4 + Tc*wdop_oporn(j)];
+
−
           
+
−
            m_I_old =  A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*cos(phi_real(1) - phi_oporn(1) + (wdop_real(1)-wdop_oporn(j))*Tc/2);
+
−
           
+
−
            m_I = A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*cos(phi_real(2) - phi_oporn(2) + (wdop_real(1)-wdop_oporn(j))*Tc/2);
+
−
           
+
−
            m_Q_old = - A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*sin(phi_real(1) - phi_oporn(1) + (wdop_real(1)-wdop_oporn(j))*Tc/2);
+
−
           
+
−
            m_Q = - A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*sin(phi_real(2) - phi_oporn(2) + (wdop_real(1)-wdop_oporn(j))*Tc/2);
+
−
           
+
−
            I_old = m_I_old + n_I_old;
+
−
            I = m_I + n_I;
+
−
            Q_old = m_Q_old + n_Q_old;
+
−
            Q = m_Q + n_Q;
+
−
           
+
−
            UdFLL(1, j) = UdFLL(1,j) + I*Q_old - Q*I_old;
+
−
        end
+
−
        if ~mod(k, N/10)
+
−
            fprintf('Progress %d%%\n', k*100/N)
+
−
        end
+
−
    end
+
−
   
+
−
    UdFLL_mean = A_IQ^2*(sinc((wdop_real(1)-wdop_oporn)*Tc/2 /pi)).^2.*sin((wdop_real(1)-wdop_oporn)*Tc);
+
−
   
+
−
    UdFLL = UdFLL/N;
+
−
   
+
−
    figure
+
−
    plot((wdop_real-wdop_oporn)/2/pi,[UdFLL; UdFLL_mean; Sd*(wdop_real-wdop_oporn)]);
+
−
    ylim([1.1*min(UdFLL_mean) 1.1*max(UdFLL_mean)])
+
−
    grid on;
+
−
    xlabel('\Delta f, Гц')
+
−
    ylabel('M[u_{Д}]')
+
−
    title(['q = ' num2str(qcno_dB) ' дБГц, T = ' num2str(Tc) ' c'])
+
−
end
+
  
−
if plotFX
+
== Ссылки ==
−
    N = 5000;
+
<references/>
−
    stdn_IQ = 8;
+
−
    Tc = 0.02;
+
−
    qcno_dB = [10:1:50];
+
−
    wdop_real = [2*pi*100];
+
−
    wdop_oporn = [2*pi*100];
+
−
   
+
−
    D_etta_FLL = zeros(1,length(qcno_dB));
+
−
    CKO_etta_FLL_teor = nan(1,length(qcno_dB));
+
−
   
+
−
    for i = 1:length(qcno_dB)
+
−
        fprintf('qcno_dB = %.0f\n', qcno_dB(i));
+
−
        qcno = 10^(qcno_dB(i)/10);
+
−
        A_IQ = stdn_IQ * sqrt(2 * qcno * Tc);
+
−
       
+
−
        UdFLL = nan(1, N);
+
−
       
+
−
        for k = 1:N
+
−
           
+
−
            for j = 1:length(wdop_oporn)
+
−
                n_I_old = 1*stdn_IQ * randn(1,1);
+
−
                n_I = 1*stdn_IQ * randn(1,1);
+
−
                n_Q_old = 1*stdn_IQ * randn(1,1);
+
−
                n_Q = 1*stdn_IQ * randn(1,1);
+
−
               
+
−
                phi_real = [pi/3 pi/3 + Tc*wdop_real(1)];
+
−
                phi_oporn =[pi/4 pi/4 + Tc*wdop_oporn(j)];
+
−
                m_I_old =  A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*cos(phi_real(1) - phi_oporn(1) + (wdop_real(1)-wdop_oporn(j))*Tc/2);
+
−
               
+
−
                m_I = A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*cos(phi_real(2) - phi_oporn(2) + (wdop_real(1)-wdop_oporn(j))*Tc/2);
+
−
               
+
−
                m_Q_old = - A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*sin(phi_real(1) - phi_oporn(1) + (wdop_real(1)-wdop_oporn(j))*Tc/2);
+
−
               
+
−
                m_Q = - A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*sin(phi_real(2) - phi_oporn(2) + (wdop_real(1)-wdop_oporn(j))*Tc/2);
+
−
               
+
−
                I_old = m_I_old + n_I_old;
+
−
                I = m_I + n_I;
+
−
                Q_old = m_Q_old + n_Q_old;
+
−
                Q = m_Q + n_Q;
+
−
               
+
−
                UdFLL(1, k) = I*Q_old - Q*I_old;
+
−
            end
+
−
        end
+
−
        D_etta_FLL(1,i) = mean((UdFLL - mean(UdFLL)).^2);
+
−
       
+
−
        CKO_etta_FLL(1,i) = sqrt(D_etta_FLL(1,i));
+
−
        CKO_etta_FLL_teor(1,i) = sqrt((A_IQ^2*Tc)^2*(1/(qcno*Tc^3))*(1 + 1/(2*qcno*Tc)));
+
−
    end
+
−
    figure
+
−
    plot(qcno_dB, CKO_etta_FLL, 'r*', qcno_dB, CKO_etta_FLL_teor, 'g')
+
−
    xlabel('q_c/n0, дБГц')
+
−
    ylabel('\sigma_{вых} ЧД')
+
−
    grid on
+
−
end
+
−
</source>
+
−
|frame-style = border:1px solid Plum
+
−
|title-style = color:black;background-color:lavender;font-weight:bold;text-align:left
+
−
|content-style = color:black;background-color:ghostwhite;text-align:center
+
−
|hidden = yes
+
−
}}
+
  
 
[[Категория:Дискриминаторы]]
 
[[Категория:Дискриминаторы]]
 
[[Категория:Оценивание частоты]]
 
[[Категория:Оценивание частоты]]

Текущая версия на 15:27, 3 ноября 2015

Содержание

Дискриминатор описывается выражением

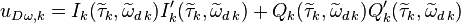u_{D \omega, k} = I_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k})I'_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) + Q_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k})Q'_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}),

где
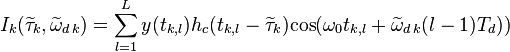I_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)\mbox{cos}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d)),
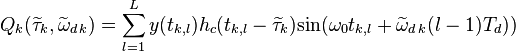Q_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)\mbox{sin}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d)),
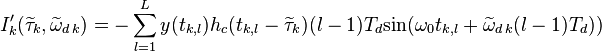I'_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = -\sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)(l-1)T_d\mbox{sin}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d)),
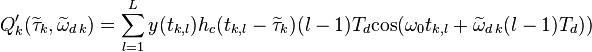Q'_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)(l-1)T_d\mbox{cos}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d)),
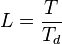L=\frac{T}{{{T}_{d}}} - число отсчетов за время 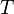T интегрирования в корреляторе, 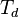T_d - интервал дискретизации.

[править] Особенности работы

Для работы дискриминатора требуется формирование особенных квадратур 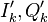I'_k, Q'_k. Они представляют собой обычные квадратуры, умноженные на линейно-возрастающую функцию 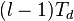(l-1)T_d (индекс времени 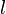l растет - множитель растет). Аппаратно такой коррелятор не реализован. Есть предложение [1] заменить честный расчет 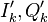I'_k, Q'_k суммой взвешенных корреляционных сумм:

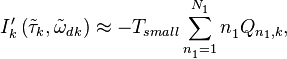
I'_{k}\left( {{{\tilde{\tau }}}_{k}},{{{\tilde{\omega }}}_{{{d}^{{}}}k}} \right)\approx -{{T}_{small}}\sum\limits_{n_{1}^{{}}=1}^{N_{1}^{{}}}{n_{1}^{{}}{{Q}_{{{n}_{1}},k}}},
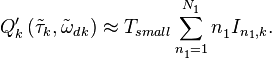
Q'_{k}\left( {{{\tilde{\tau }}}_{k}},{{{\tilde{\omega }}}_{{{d}^{{}}}k}} \right)\approx {{T}_{small}}\sum\limits_{n_{1}^{{}}=1}^{N_{1}^{{}}}{n_{1}^{{}}{{I}_{{{n}_{1}},k}}}.

По этой методике весь интервал интегрирования в корреляторе разбивается на 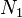N_1 равных частей длительностью 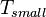T_{small}. На этих малых интервалах рассчитываются традиционные корреляционные суммы 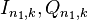I_{n_1, k}, Q_{n_1, k}, а потом проводится их взвешенное суммирование. Чем больше 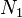N_1, тем точнее оказывается приведенная методика. Допустим "большой" коррелятор копит 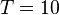T = 10 мс, тогда целесообразно выбрать T_{small} = 1 мс и N_1 = 10.

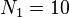[править] Дискриминационная характеристика

Дискриминационная характеристика [1]:


U\left( \delta \omega \right)=A_{IQ}^{2}T\frac{\text{sinc}\left( \frac{\delta \omega T}{2} \right)}{\delta \omega T}\left( \text{sinc}\left( \frac{\delta \omega T}{2} \right)-\cos \left( \frac{\delta \omega T}{2} \right) \right),

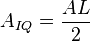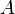где A_{IQ} = \frac{AL}{2}, A - амплитуда сигнала 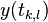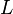y(t_{k,l}), L - количество отчетов, накапливаемых в корреляторе, 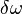\delta\omega - разность истинного и опорного параметров.


Крутизна при нулевой ошибке по частоте [1]:

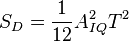
S_D=\frac{1}{12}A_{IQ}^{2}{{T}^{2}}


Вид дискриминационной характеристики для разных времен накопления и 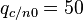q_{c/n0} = 50 дБГц:

20151103 FreqDiskr.png

[править] Флуктуационная характеристика

Дисперсия шума эквивалентного наблюдения частоты, т.е. шума с выхода дискриминатора, пересчитанного к его входу при нулевой расстройке по частоте [2]:

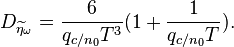
D_{\widetilde{\eta}_\omega} = \frac{6}{q_{c/n_0}T^3}(1+\frac{1}{q_{c/n_0}T}).

[править] Сравнение с другими ЧД

Интересно сравнить дисперсию шумов по входу для различных дискриминаторов:

D_1 = D_{\widetilde{\eta}_\omega} = \frac{1}{q_{c/n_0}T_{1}^3}(1+\frac{1}{2q_{c/n_0}T_{1}}).
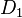  • Дисперсия шума на входе рассматриваемого в этой статье дискриминатора:
D_2 = D_{\widetilde{\eta}_\omega} = \frac{6}{q_{c/n_0}T_{2}^3}(1+\frac{1}{q_{c/n_0}T_{2}}).

Пусть cross дискриминатор реализован по схеме без перекрытия, тогда 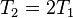T_{2} = 2T_{1} и

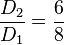\frac{D_2}{D_1} = \frac{6}{8},

или для СКО:

\sigma_2 = 0.866*\sigma_1.

Дискриминатор cross проигрывает 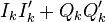I_kI'_k+Q_kQ'_k около 15% по СКО во всем диапазоне с/ш. На рисунке ниже приведен график зависимости СКО эквивалентных шумов представленных ЧД от отношения сигнал/шум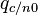 q_{c/n0}

Ошибка создания миниатюры: convert: unable to open image `/app/images/0/07/20151029__.png': No such file or directory @ error/blob.c/OpenBlob/2641.
convert: no images defined `/tmp/transform_3d19cbb41254-1.png' @ error/convert.c/ConvertImageCommand/3044.


Далее построены нормированные на крутизну дискриминационные характеристики сравниваемых дискриминаторов. Как и при сравнении дисперсий шума, полагаем 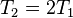T_2 = 2T_1.

20151103 FreqDiskrCompare.png


Из приведенного рисунка следует вывод, что апертура обоих частотных дискриминаторов равна
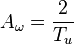A_\omega=\frac{2}{T_u}.
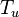T_u - темп работы дискриминатора. Ранее дискриминаторы сравнивались при условии 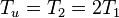T_u = T_2 = 2T_1, т.е. при одинаковом темпе работы. При анализе "cross" дискриминатора нужно помнить, что 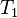T_1 в формулах его характеристик - это время когерентного накопления в корреляторе, а темп работы самого дискриминатора по схеме без перекрытия T_u = 2T_1.

[править] Листинг модели

[править] Ссылки

  1. ↑ 1,0 1,1 1,2 Публикация:Корогодин 2013 Разработка алгоритмов обработки сигналов СНС в аппаратуре определения угловой ориентации объектов
  2. ↑ Публикация:Корогодин 2013 Потенциальные характеристики оценивания частоты в некогерентном приемнике
Источник — «https://2fwww.srns.ru/index.php?title=Дискриминатор_частоты_оптимальный_при_малом_отношении_сигнал/шум&oldid=13855»
Персональные инструменты
Пространства имён

Варианты
Действия
SRNS Wiki
Рабочие журналы
Приватный файлсервер
QNAP Сервер
Инструменты