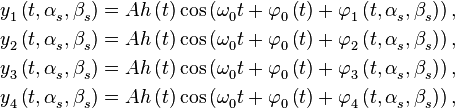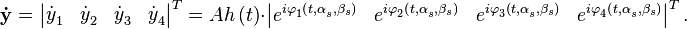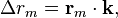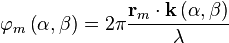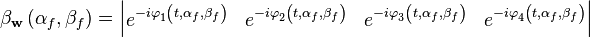Задания к практическим занятиям (ММ РУиС) — различия между версиями
Korogodin (обсуждение | вклад) (→Задача 1.2 Расчет доплеровского сдвига навигационного сигнала) |
Korogodin (обсуждение | вклад) (→Задача 3.1 Сигналы и диаграмма направленности антенной решетки) |
||
| (не показаны 62 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
== Занятие 1 == | == Занятие 1 == | ||
| − | '''Тема занятия:''' Использование системы контроля версий. | + | '''Тема занятия:''' Использование системы контроля версий. Моделирование RC-цепи. |
'''Цели занятия:''' | '''Цели занятия:''' | ||
| Строка 48: | Строка 48: | ||
# На странице проекта выбираем ''Project Home > People > Add member''. | # На странице проекта выбираем ''Project Home > People > Add member''. | ||
| − | # Вводим адреса электронной почты gmail преподавателей, например, <code> | + | # Вводим адреса электронной почты gmail преподавателей, например, <code>korogodiniv@gmail.com</code>. |
# Не изменяем статус - ''Commiter'', нажимаем кнопку ''Add members'' | # Не изменяем статус - ''Commiter'', нажимаем кнопку ''Add members'' | ||
| Строка 55: | Строка 55: | ||
==== Шаг 4. Получить рабочую копию на локальный компьютер ==== | ==== Шаг 4. Получить рабочую копию на локальный компьютер ==== | ||
| − | Для загрузки рабочей копии проекта с сервера на локальный компьютер используется команда <code>svn checkout</code>. Рабочие каталоги пользователей следует размещать в директории <code>/home/student/Modeling</code>. Пример команды ( | + | '''Для пользователей Subversion (GNU/Linux)''' |
| + | |||
| + | Для загрузки рабочей копии проекта с сервера на локальный компьютер используется команда <code>svn checkout</code>. Рабочие каталоги пользователей следует размещать в директории <code>/home/student/Modeling</code>. Пример команды (вводится в окно терминала, например, konsole): | ||
<source lang="bash">svn checkout https://mm-er09-ivanov-ii.googlecode.com/svn/trunk/ /home/student/Modeling/mm-er09-ivanov-ii --username er09.ivanov.ii@gmail.com</source> | <source lang="bash">svn checkout https://mm-er09-ivanov-ii.googlecode.com/svn/trunk/ /home/student/Modeling/mm-er09-ivanov-ii --username er09.ivanov.ii@gmail.com</source> | ||
где <code>mm-er09-ivanov-ii</code> - название проекта, <code>er09.ivanov.ii</code> - логин пользователя. | где <code>mm-er09-ivanov-ii</code> - название проекта, <code>er09.ivanov.ii</code> - логин пользователя. | ||
| Строка 61: | Строка 63: | ||
Подсмотреть синтаксис команды можно на веб-странице проекта на вкладке ''Source > Checkout'' | Подсмотреть синтаксис команды можно на веб-странице проекта на вкладке ''Source > Checkout'' | ||
| − | ==== Шаг 5. Создать структуру каталогов | + | |
| + | '''Для пользователей TortoiseSVN (Windows)''' | ||
| + | |||
| + | Для получения новой рабочей копии используется функция ''SVN Checkout'' (''SVN Извлечь''), вызываемая в контекстном меню после нажатия правой кнопкой мыши в требуемой папке. | ||
| + | [[file:201302_SVN1.png|center]] | ||
| + | |||
| + | В открывшемся окне вводится адрес хранилища и имя папки на компьютере, в которой будет расположена рабочая копия. | ||
| + | [[file:201302_SVN2.png|center]] | ||
| + | |||
| + | После нажатия кнопки ''Ok'' происходит загрузка последней ревизии на локальную машину. | ||
| + | [[file:201302_SVN3.png|center]] | ||
| + | |||
| + | ==== Шаг 5. Создать структуру каталогов ==== | ||
В каталоге проекта будут храниться файлы всех практических и лабораторных занятий: отчеты, скрипты, графики. | В каталоге проекта будут храниться файлы всех практических и лабораторных занятий: отчеты, скрипты, графики. | ||
| − | + | В файловом менеджере операционной системы создаем директории в рабочем каталоге: | |
<source lang="bash"> | <source lang="bash"> | ||
/lab | /lab | ||
| Строка 83: | Строка 97: | ||
</source> | </source> | ||
| − | + | ==== Шаг 6. Добавить файлы/каталоги под систему контроля версий ==== | |
| − | + | Созданы директории внутри рабочего каталога, но система контроля версий ещё не знает об их существовании, не следит за их изменениями. Необходимо занести директории под контроль SVN'а. | |
| − | + | '''Для пользователей Subversion/RabbitVCS (GNU/Linux)''' | |
| − | === Задача 1.2 Расчет доплеровского сдвига навигационного сигнала === | + | Добавляем каталоги под контроль версий с помощью кнопки ''Add'' в контекстном меню RabbitVCS (аналог консольной команды <code>svn add</code>, вызывается нажатием правой кнопки в файловом менеджере). |
| + | [[file:201302_SVN5.png|center]] | ||
| + | |||
| + | RabbitVCS - графический интерфейс к программе Subversion, установленный в наших лабораториях. Популярный аналог для систем семейства Windows - TortoiseSVN. Пользователи MacOS могут обратить внимание на SmartSVN. | ||
| + | |||
| + | '''Для пользователей TortoiseSVN (Windows)''' | ||
| + | |||
| + | Добавляем каталоги под контроль версий с помощью кнопки ''Add'' (''Добавить'') в контекстном меню TortoiseVCS (вызывается нажатием правой кнопки в файловом менеджере). | ||
| + | [[file:201302_SVN4.png|center]] | ||
| + | |||
| + | ==== Шаг 7. Сделать первый коммит ==== | ||
| + | |||
| + | После выполнения команды ''Add'' (''Добавить'') файлы (каталоги в нашем случае) добавляются в рабочую копию проекта. Командой <code>svn commit</code> (или аналогичной кнопкой в RabbitVCS, TortoiseSVN) производится так называемый "коммит" - добавление новой ревизии на сервер путем отправки туда вашей рабочей копии. Вводится логин вида <code>er09.ivanov.ii@gmail.com</code>, пароль с вкладки ''Profile > Settings > GoogleCode.com Password'' веб-страницы аккаунта. | ||
| + | |||
| + | '''В RabbitVCS (GNU/Linux):''' | ||
| + | [[file:201302_SVN6.png|center]] | ||
| + | |||
| + | '''В TortoiseSVN (Windows):''' | ||
| + | [[file:201302_SVN7.png|center]] | ||
| + | |||
| + | Теперь в веб-интерфейсе проекта на вкладке ''Source > Browse'' можно наблюдать появление новой ревизии и состояние проекта, ей соответствующее. При этом вы имеете возможность просмотреть и предыдущие ревизии, а если понадобиться - получить их на свой компьютер. | ||
| + | |||
| + | === Задача 1.2 Получить задание к лабораторной работе 1, разобрать на примере RC-цепи === | ||
| + | |||
| + | Тема первой лабораторной - моделирование методом несущей на примере электрических цепей. В рамках домашней подготовки от студентов требуется формализовать постановку задачи (объект, его границы при моделировании, цель исследования), записать математическую модель, предложить тестовое воздействие, составить блок-схему программы модели. | ||
| + | |||
| + | В рамках практического задания предлагается разобрать подготовку к лабораторной работе на примере примере RC-цепи. | ||
| + | |||
| + | Файлы модели хранить в каталоге praxis/1. Сделать несколько коммитов во время и по завершению работы. | ||
| + | |||
| + | == Занятие 2 == | ||
| + | |||
| + | '''Тема занятия:''' Доплеровский сдвиг навигационного сигнала. Описание сигналов антенной решетки. | ||
| + | |||
| + | '''Цели занятия:''' | ||
| + | * развить навыки моделирования: использование векторов, цикл по времени, обработка результатов моделирование, построение графиков и гистограмм. | ||
| + | |||
| + | === Задача 2.1 Расчет доплеровского сдвига навигационного сигнала === | ||
| + | |||
| + | '''Постановка задачи:''' | ||
Автомобильный навигатор является классическим радиоприемным устройством класса ''аппаратура потребителей спутниковых радионавигационных систем''. В процессе своей работы он принимает сигналы от навигационных спутников, оценивает их параметры, выделяет навигационное сообщение, заложенное в сигналах, и, в итоге, решает навигационную задачу - определяет своё местоположение. | Автомобильный навигатор является классическим радиоприемным устройством класса ''аппаратура потребителей спутниковых радионавигационных систем''. В процессе своей работы он принимает сигналы от навигационных спутников, оценивает их параметры, выделяет навигационное сообщение, заложенное в сигналах, и, в итоге, решает навигационную задачу - определяет своё местоположение. | ||
| Строка 95: | Строка 148: | ||
Так как навигационные спутники относительно планеты находятся в постоянном движении, да и из-за движения потребителя, возникает эффект Доплера - происходит смещение частоты принимаемого сигнала от номинала. Интересно, в каких пределах может находиться это смещение для неподвижного приемника? Какова гистограмма возможных значений? | Так как навигационные спутники относительно планеты находятся в постоянном движении, да и из-за движения потребителя, возникает эффект Доплера - происходит смещение частоты принимаемого сигнала от номинала. Интересно, в каких пределах может находиться это смещение для неподвижного приемника? Какова гистограмма возможных значений? | ||
| − | + | '''Комментарии:''' | |
| + | |||
| + | Связь [https://ru.wikipedia.org/wiki/Эффект_Доплера доплеровского сдвига] и скорости по линии визирования известна каждому радиотехнику: | ||
| + | :<math>\frac{f_d}{f_0} = \frac{V}{c}</math>. | ||
| + | |||
| + | Несущая частота <math>f_0</math> радионавигационного сигнала известна, задается ИКД. Скорость света <math>c</math> - фундаментальная константа. Остается определить скорость по линии визирования <math>V</math>. | ||
| + | |||
| + | Потребитель по условию задачи неподвижен. Тогда скорость по линии визирования - проекция вектора скорости спутника на линию визирования. Итого, достаточно определить два вектора - орт от спутника к потребителю и вектор скорости спутника. | ||
| + | |||
| + | Для простоты ограничимся "плоской" задачей - когда потребитель попадает на подспутниковую траекторию, угловым вращением Земли так же пренебрежем. Иллюстрация - на рисунке: | ||
| + | [[file:20140217_Z2_1_1.png|700px|center]] | ||
| + | |||
| + | Выберем СК ''XOY'' в которой потребитель расположен на оси OY, его радиус-вектор <math>\mathbf{r}_r = (0, R_e)</math>, где <math>R_e</math> - радиус Земли (учет высоты над уровнем моря для Москвы, 170-190 м, слабо повлияет на результат). | ||
| + | |||
| + | Если определим вектор спутника <math>\mathbf{r}_{sv}</math> на любой момент витка, то задача будет почти решена, останется: | ||
| + | * выбрать те положения, для которых y-координата спутника больше y-координаты потребителя (условие видимости), | ||
| + | * по приращению координат определить вектор скорости спутника <math>\mathbf{V}_{sv}</math>, | ||
| + | * вычитанием найти вектор потребитель-спутник <math>\mathbf{r}_v</math> задающий линию визирования, | ||
| + | * определить скорость сближения по линии визирования <math>V_v = - \frac{\mathbf{V}_{sv} \cdot \mathbf{r}_v }{|\mathbf{r}_v|}</math>, | ||
| + | * пересчитать скорость сближения в доплеровский сдвиг. | ||
| + | |||
| + | Определить же радиус-вектор спутника легко. Его длина известна, а скорость вращения - примерно оборот за 12 часов (у нас плоская задача, в которой мы пренебрегли различием ECEF и ECI). | ||
| + | |||
| + | Дальше - дело техники. | ||
| + | |||
| + | Шаги по усложнению модели, если результат неубедителен: | ||
| + | * учесть вращение Земли (наклонение орбит известно из ИКД), | ||
| + | * учесть случаи, когда потребитель не попадает под подспутниковую траекторию. | ||
| + | |||
| + | == Занятие 3 == | ||
| + | |||
| + | '''Тема занятия:''' Описание сигналов антенной решетки. | ||
| + | |||
| + | '''Цели занятия:''' | ||
| + | * привести пример использования метода комплексных амплитуд; | ||
| + | * изложить методику расчет диаграммы направленности антенной решетки, востребованную при подготовке ко второй лабораторной работе; | ||
| + | * освоить создание и использование собственных функций в MATLAB; | ||
| + | * освоить матричные операции; | ||
| + | * научиться визуализировать поверхности. | ||
| + | |||
| + | === Задача 3.1 Сигналы и диаграмма направленности антенной решетки === | ||
| + | |||
| + | '''Постановка задачи:''' | ||
| + | Сигнал, приходящий из дальней зоны, принимается системой пространственно разнесенных антенн - антенной решеткой. Размеры антенной решетки значительно меньше постоянной времени корреляции принимаемых сигналов (огибающая, в первом приближении, совпадает для сигналов разных антенн). | ||
| + | |||
| + | Конфигурация антенной решетки - четырехэлементная, с расположением антенных элементов в углах квадрата со стороной, равной половине длине волны. | ||
| + | |||
| + | [[file:201402_Z2_2_1.png|500px|center]] | ||
| + | |||
| + | Построить серию диаграмм направленности при фокусировке в различных направлениях (зенит, отклонение в сторону на 10, 30, 45, 60 градусов). | ||
| + | |||
| + | '''Комментарии:''' | ||
| + | |||
| + | ''Сигналы антенных элементов'' | ||
| + | |||
| + | Каждая m-я антенна формирует на выходе свой собственный сигнал <math>y_m \left( t \right)</math>. При фокусировке производят весовое сложение сигналов различных антенн, получая из нескольких сигналов один. | ||
| + | |||
| + | [[file:201402_Antenna.png|center]] | ||
| + | |||
| + | По условию задачи можно пренебречь разностью огибающей для различных точек апертуры антенны. Для ряда практических задач это допущение прекрасно выполняется. Тогда сигналы антенн отличаются только фазой несущей, их математическая модель может быть представлена в виде: | ||
| + | |||
| + | :<math>\begin{align} | ||
| + | & y_{1}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right)=Ah\left( t \right)\cos \left( \omega _{0}^{{}}t+\varphi _{0}^{{}}\left( t \right)+\varphi _{1}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right) \right), \\ | ||
| + | & y_{2}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right)=Ah\left( t \right)\cos \left( \omega _{0}^{{}}t+\varphi _{0}^{{}}\left( t \right)+\varphi _{2}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right) \right), \\ | ||
| + | & y_{3}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right)=Ah\left( t \right)\cos \left( \omega _{0}^{{}}t+\varphi _{0}^{{}}\left( t \right)+\varphi _{3}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right) \right), \\ | ||
| + | & y_{4}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right)=Ah\left( t \right)\cos \left( \omega _{0}^{{}}t+\varphi _{0}^{{}}\left( t \right)+\varphi _{4}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right) \right), \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | где <math>A</math> - амплитуда сигналов, <math>h\left( t \right)</math> - огибающая, <math>\omega _{0}</math> - несущая частота, <math>\varphi _{0}^{{}}\left( t \right)</math> - фаза в начале антенной системы координат OXYZ, <math>\varphi _{m}^{{}}\left( t , \alpha _{s}^{{}},\beta _{s}\right )</math> - фазовый набег относительно фазы в начале антенной системы координат для m-й антенны, <math>\alpha_s, \beta_s</math> - угол места и азимут направления на источник сигнала. | ||
| + | |||
| + | В рамках этой задачи удобно применить метод комплексных амплитуд. Тогда модели сигналов преобразуются к виду | ||
| + | |||
| + | :<math>y_{m}^{{}}\left( t \right)= Ah\left( t \right)\operatorname{Re}\left[ e_{{}}^{i\left( \omega _{0}^{{}}t+\varphi _{0}^{{}}\left( t \right) \right)}e_{{}}^{i\varphi _{m}^{{}}\left( t, \alpha _{s}^{{}},\beta _{s} \right)} \right]</math>, | ||
| + | |||
| + | обозначим | ||
| + | |||
| + | :<math>\dot{y}_{m}^{{}}\left( t \right)= Ah\left( t \right) e_{{}}^{i\varphi _{m}^{{}}\left( t, \alpha _{s}^{{}},\beta _{s} \right)}</math> - комплексная амплитуда сигнала m-ой антенны. | ||
| + | |||
| + | Составим вектор из комплексных амплитуд сигналов различных антенн | ||
| + | |||
| + | :<math>\mathbf{\dot{y}}_{{}}^{{}}=\left| \begin{matrix} | ||
| + | \dot{y}_{1}^{{}} & \dot{y}_{2}^{{}} & \dot{y}_{3}^{{}} & \dot{y}_{4}^{{}} \\ | ||
| + | \end{matrix} \right|_{{}}^{T}=Ah\left( t \right)\cdot \left| \begin{matrix} | ||
| + | e_{{}}^{i\varphi _{1}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s} \right)} & e_{{}}^{i\varphi _{2}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s} \right)} & e_{{}}^{i\varphi _{3}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s} \right)} & e_{{}}^{i\varphi _{4}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s} \right)} \\ | ||
| + | \end{matrix} \right|_{{}}^{T}.</math> | ||
| + | |||
| + | Вектор комплексных амплитуд при приеме образуется после гетеродинирования сигналов (в передающих устройствах последовательность обратная). | ||
| + | |||
| + | |||
| + | ''Связь фазовых набегов с направлением на источник сигнала'' | ||
| + | |||
| + | Фазовый набег относительно фазы в начале антенной системы координат определяется положением антенного элемента и направлением прихода сигнала. Его легко рассчитать зная орт <math>\mathbf{k}</math> на источник и радиус-вектор <math>\mathbf{r}_m</math> антенного элемента. | ||
| + | |||
| + | [[file:201402_Z2_2_2.png|600px|center]] | ||
| + | |||
| + | Разность хода фазового фронта сигнала <math>\Delta r_m</math> есть скалярное произведение орта и радиус-вектора точки пространства | ||
| + | :<math>\Delta r_m = \mathbf{r}_m \cdot \mathbf{k},</math> | ||
| + | |||
| + | фазовый набег связан с разностью хода фазового фронта через длину волны несущей сигнала | ||
| + | :<math>\varphi_m = 2 \pi \frac{\Delta r_m}{\lambda}</math>. | ||
| + | |||
| + | Для m-oй антенны и направления <math>\alpha, \beta</math> получаем выражение | ||
| + | |||
| + | :<math>{{\varphi }_{m}}\left( \alpha ,\beta \right)=2\pi \frac{{{\mathbf{r}}_{m}}\cdot \mathbf{k}\left( \alpha ,\beta \right)}{\lambda }</math> | ||
| + | |||
| + | |||
| + | ''Алгоритм фокусировки'' | ||
| + | |||
| + | При фокусировке антенны в направлении углов <math>\alpha_f, \beta_f</math> производится умножение вектора-строки фокусировки на вектор-столбец комплексных сигналов | ||
| + | |||
| + | :<math>\dot{U}=\mathbf{\beta_w }\left( \alpha _{f}^{{}},\beta _{f}^{{}} \right)\mathbf{\dot{y}}\left( \alpha _{s}^{{}},\beta _{s}^{{}} \right)_{{}}^{{}}</math>. | ||
| + | |||
| + | Вектор фокусировки определяется ожидаемыми фазовыми набегами для направления фокусировки | ||
| + | |||
| + | :<math>\mathbf{\beta_w }\left( \alpha_f ,\beta_f \right)=\left| \begin{matrix} | ||
| + | e_{{}}^{-i\varphi _{1}^{{}}\left( t,\alpha_f ,\beta_f \right)} & e_{{}}^{-i\varphi _{2}^{{}}\left( t,\alpha_f ,\beta_f \right)} & e_{{}}^{-i\varphi _{3}^{{}}\left( t,\alpha_f ,\beta_f \right)} & e_{{}}^{-i\varphi _{4}^{{}}\left( t,\alpha_f ,\beta_f \right)} \\ | ||
| + | \end{matrix} \right|</math> | ||
| + | |||
| + | |||
| + | ''Диаграмма направленности'' | ||
| + | |||
| + | ''Характеристикой направленности'' называют зависимость нормированной комплексной амплитуды | ||
| + | <math>\frac{\dot{U}\left( \alpha _{s}^{{}},\beta _{s}^{{}}|\alpha _{f}^{{}},\beta _{f}^{{}} \right)}{A_i h\left( t \right)}</math> | ||
| + | на выходе системы пространственной обработки от направления прихода пробного сигнала <math>\alpha_s,\beta_s</math> при заданном направлении фокусировки <math>\alpha_f,\beta_f</math>. Здесь <math>A_i</math> - амплитуда одного сигнала на выходе всенаправленной антенны. | ||
| + | |||
| + | Функция | ||
| + | <math>F\left( \alpha _{s}^{{}},\beta _{s}^{{}}|\alpha _{f}^{{}},\beta _{f}^{{}} \right)=\left| \frac{\dot{U}\left( \alpha _{s}^{{}},\beta _{s}^{{}}|\alpha _{f}^{{}},\beta _{f}^{{}} \right)}{A_ih\left( t \right)} \right|_{{}}^{2}</math> | ||
| + | называется ''диаграммой направленности''. | ||
| + | |||
| + | Для принятой модели сигналов диаграмма направленности определяется выражением: | ||
| + | :<math>F\left( \alpha _{s}^{{}},\beta _{s}^{{}}|\alpha _{f}^{{}},\beta _{f}^{{}} \right)=F_{am}^{{}}\left( \alpha _{s}^{{}},\beta _{s}^{{}} \right)\left| \mathbf{\beta }\left( \alpha _{f}^{{}},\beta _{f}^{{}} \right)\cdot \left| \begin{matrix} | ||
| + | e_{{}}^{i\varphi _{1}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right)} & e_{{}}^{i\varphi _{2}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right)} & e_{{}}^{i\varphi _{3}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right)} & e_{{}}^{i\varphi _{4}^{{}}\left( t,\alpha _{s}^{{}},\beta _{s}^{{}} \right)} \\ | ||
| + | \end{matrix} \right|_{{}}^{T} \right|_{{}}^{2}</math>, | ||
| + | |||
| + | где <math>F_{am}^{{}}\left( \alpha _{s}^{{}},\beta _{s}^{{}} \right)</math> - диаграмма направленности одного антенного элемента. | ||
| + | |||
| + | |||
| + | ''Вывод диаграммы направленности в трехмерном виде'' | ||
| + | |||
| + | Результатом вычислений диаграммы направленности является массив значений <math>F\left( \alpha _{s}^{{}},\beta _{s}^{{}}|\alpha _{f}^{{}},\beta _{f}^{{}} \right)</math> для угла <math>\alpha_s</math> от -180 до 180 градусов, <math>\beta_s</math> от -90 до 90 (данный выбор диапазона углов не соответствует традиционному определению сферических координат, зато удобен для вывода диаграммы направленности): | ||
| + | <source lang="matlab"> | ||
| + | alpha = deg2rad(-180:2:180); | ||
| + | beta = deg2rad(-90:2:90); | ||
| + | ... | ||
| + | F | ||
| + | </source> | ||
| + | |||
| + | Для задания поверхности недостаточно задать массивы координат её точек, т.к. нужна информация о том, какие точки являются соседними - что с чем соединять. Поэтому в MATLAB используются не три вектора координат, а три матрицы, задающие сетку параметров. | ||
| + | |||
| + | [[file:201402_Z2_2_3.png|center|500px]] | ||
| + | |||
| + | Для "растягивания" векторов координат абсцисс и ординат используется функция meshgrid | ||
| + | <source lang="matlab"> | ||
| + | [alpha_m, beta_m] = meshgrid(alpha, beta); | ||
| + | </source> | ||
| + | |||
| + | Значения <math>\alpha_s</math>, <math>\beta_s</math>, <math>F</math> задают три координаты в сферической системе координат. В MATLAB доступны функции построения поверхностей в прямоугольной декартовой системе координат, поэтому перед построением необходимо произвести соответствующее преобразование. Для преобразования из сферической в прямоугольную систему существует функция <code>[x, y, z] = sph2cart(beta_m, alpha_m, F)</code>, производящая отображение: | ||
| + | <source lang="matlab"> | ||
| + | x = F .* cos(alpha_m) .* cos(beta_m); | ||
| + | y = F .* cos(alpha_m) .* sin(beta_m); | ||
| + | z = F .* sin(alpha_m); | ||
| + | </source> | ||
| + | |||
| + | Для вывода поверхности используется функция <code>surf(x, y, z)</code> | ||
| + | <source lang="matlab"> | ||
| + | figure(1); | ||
| + | surf(x, y, z); | ||
| + | xlabel('x'); ylabel('y'); zlabel('z'); | ||
| + | </source> | ||
| + | |||
| + | Для лучшего восприятия следует сделать равные пределы по всем трем осям | ||
| + | <source lang="matlab"> | ||
| + | minc = min( [min(min(x)) min(min(y)) min(min(z))] ); | ||
| + | maxc = max( [max(max(x)) max(max(y)) max(max(z))] ); | ||
| + | xlim([minc maxc]); ylim([minc maxc]); zlim([minc maxc]); | ||
| + | </source> | ||
| + | |||
| + | Например, для четвертьволнового вибратора | ||
| + | <source lang="matlab"> | ||
| + | F = abs(cos(alpha_m).*1); | ||
| + | </source> | ||
| + | вывод диаграммы направленности | ||
| + | [[file:201402_Z2_2_4.png|center]] | ||
| + | |||
[[Категория:ММ РУиС (дисциплина)]] | [[Категория:ММ РУиС (дисциплина)]] | ||
Текущая версия на 11:41, 12 марта 2014
[править] Занятие 1
Тема занятия: Использование системы контроля версий. Моделирование RC-цепи.
Цели занятия:
- Создать студенческие репозитории (хранилища) на Google Code.
- Познакомить студентов с системой контроля версий Subversion (SVN), включая программы-клиенты
- Познакомить студентов с MATLAB/Octave: интерфейс, переменные, векторы, матрицы, вывод графиков, написание скриптов.
- Привести пример решения детерминированной математической задачи с помощью компьютерной модели.
[править] Задача 1.1 Использование системы контроля версий
При выполнении практических и лабораторных заданий, а так же домашней подготовке к ним, студенты должны пользоваться личным репозиторием SVN. Для простоты и общности предлагается создавать проекты на Google Code. Это бесплатный сервис для создания собственных репозиториев различных систем контроля версий. Из плюсов - простота, бесплатность, доступность. Минус - ограничение на лицензирование.
[править] Шаг 1. Регистрация аккаунта на googlecode.com
- Переходим на страницу https://googlecode.com.
- Если уже авторизован другой пользователь - нажимаем кнопку Sign out в правом верхнем углу.
- Переходим на страницу авторизации путем нажатия кнопки Sign in в правом верхнем углу, либо Sign in to create a project по центру.
- Выбираем Create an account (если в памяти браузера остались данные о старом пользователе, то потребуется более длинная цепочка Manage accounts on this device > Add account > Create an account)
- В поле First Name и Last Name студент указывает имя и фамилию соответственно (транслитом, как в загранпаспорте), либо произвольную информацию по собственному усмотрению.
- Имя почтового ящика указывается по шаблону:
er09.ivanov.ii@gmail.com, где09- номер потока,ivanov- фамилия студент,ii- инициалы имени и отчества студента. - Пароль выбирается студентом
- Данные о Дне рождения, телефоне, другом почтовом ящике, стране указываются по желанию студента.
- Подтверждается согласие с Google Terms of Service и Privacy Policy путем отметки check-box'а, после чего осуществляется переход на следующую страницу кнопкой Next step.
- Выбор аватара можно пропустить нажатием кнопки Next step.
Аккаунт создан.
[править] Шаг 2. Создание репозитория
Репозиторий, хранилище - место, где хранятся и поддерживаются какие-либо данные. В рамках курса ММ РТУиС каждый студент будет использовать личный репозиторий системы контроля версий SVN, предоставляемый сервисом Google Code.
- Возвращаемся на страницу https://googlecode.com. Выбираем Create a new project.
- Заполняем поля:
- Project name:
mm-er09-ivanov-ii, гдеmm- математическое моделирование,09- номер потока,ivanov- фамилия студента,ii- инициалы имени и отчества - Project summary: "Modeling of radio systems and signals" (или другое по собственному усмотрению)
- Description: "Modeling of radio systems and signals: master course" (или другое по собственному усмотрению)
- Version control system: Subversion
- Source code license: на усмотрение студента
- Project label(s): matlab, radio, signals (или другое по собственному усмотрению)
- Ввести капчу
- Project name:
- Создать репозиторий нажатием кнопки Create project
[править] Шаг 3. Пригласить преподавателей участвовать в проекте
Системы контроля версий созданы не только и не столько для того, чтобы иметь всю историю изменения проекта, а для совместной работы над ним группой. Пригласим поучаствовать во вновь созданном проекте преподавателей.
- На странице проекта выбираем Project Home > People > Add member.
- Вводим адреса электронной почты gmail преподавателей, например,
korogodiniv@gmail.com. - Не изменяем статус - Commiter, нажимаем кнопку Add members
Аккаунты преподавателей добавились в список Project People, теперь они могут следить за проектом, вносить в него правки при необходимости.
[править] Шаг 4. Получить рабочую копию на локальный компьютер
Для пользователей Subversion (GNU/Linux)
Для загрузки рабочей копии проекта с сервера на локальный компьютер используется команда svn checkout. Рабочие каталоги пользователей следует размещать в директории /home/student/Modeling. Пример команды (вводится в окно терминала, например, konsole):
где mm-er09-ivanov-ii - название проекта, er09.ivanov.ii - логин пользователя.
Подсмотреть синтаксис команды можно на веб-странице проекта на вкладке Source > Checkout
Для пользователей TortoiseSVN (Windows)
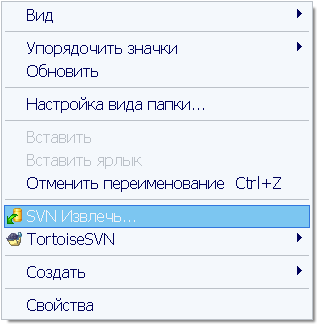
Для получения новой рабочей копии используется функция SVN Checkout (SVN Извлечь), вызываемая в контекстном меню после нажатия правой кнопкой мыши в требуемой папке.
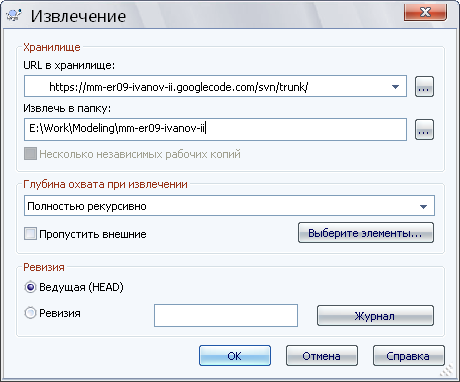
В открывшемся окне вводится адрес хранилища и имя папки на компьютере, в которой будет расположена рабочая копия.
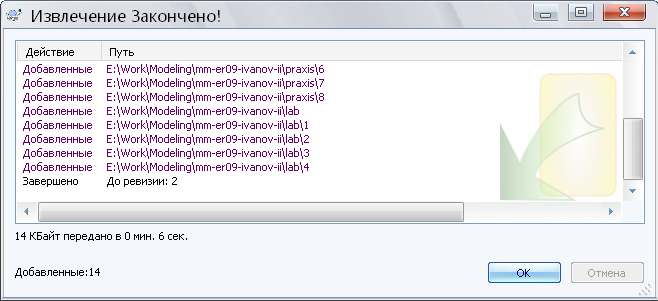
После нажатия кнопки Ok происходит загрузка последней ревизии на локальную машину.
[править] Шаг 5. Создать структуру каталогов
В каталоге проекта будут храниться файлы всех практических и лабораторных занятий: отчеты, скрипты, графики.
В файловом менеджере операционной системы создаем директории в рабочем каталоге:
..../1
..../2
..../3
..../4
/praxis
......./1
......./2
......./3
......./4
......./5
......./6
......./7
......./8
[править] Шаг 6. Добавить файлы/каталоги под систему контроля версий
Созданы директории внутри рабочего каталога, но система контроля версий ещё не знает об их существовании, не следит за их изменениями. Необходимо занести директории под контроль SVN'а.
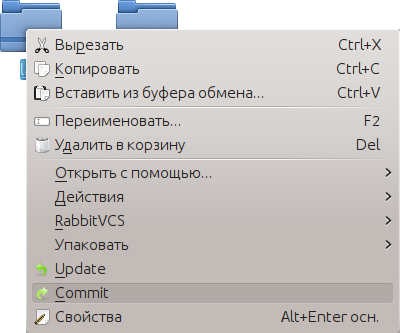
Для пользователей Subversion/RabbitVCS (GNU/Linux)
Добавляем каталоги под контроль версий с помощью кнопки Add в контекстном меню RabbitVCS (аналог консольной команды svn add, вызывается нажатием правой кнопки в файловом менеджере).
RabbitVCS - графический интерфейс к программе Subversion, установленный в наших лабораториях. Популярный аналог для систем семейства Windows - TortoiseSVN. Пользователи MacOS могут обратить внимание на SmartSVN.
Для пользователей TortoiseSVN (Windows)
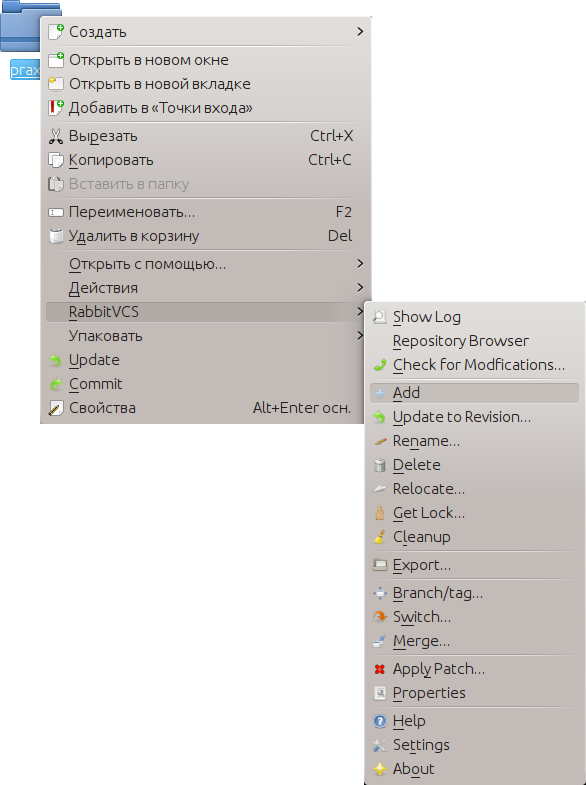
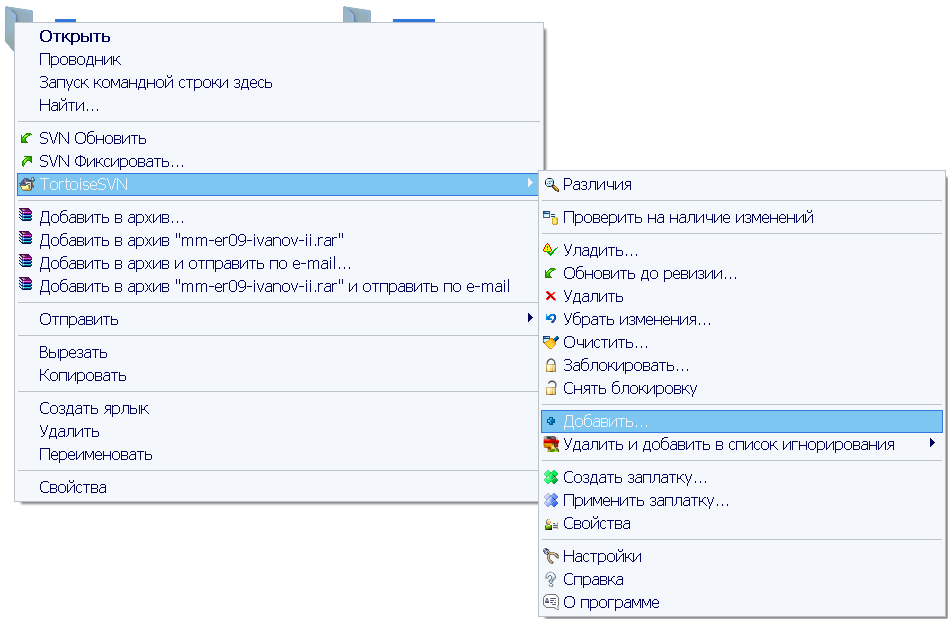
Добавляем каталоги под контроль версий с помощью кнопки Add (Добавить) в контекстном меню TortoiseVCS (вызывается нажатием правой кнопки в файловом менеджере).
[править] Шаг 7. Сделать первый коммит
После выполнения команды Add (Добавить) файлы (каталоги в нашем случае) добавляются в рабочую копию проекта. Командой svn commit (или аналогичной кнопкой в RabbitVCS, TortoiseSVN) производится так называемый "коммит" - добавление новой ревизии на сервер путем отправки туда вашей рабочей копии. Вводится логин вида er09.ivanov.ii@gmail.com, пароль с вкладки Profile > Settings > GoogleCode.com Password веб-страницы аккаунта.
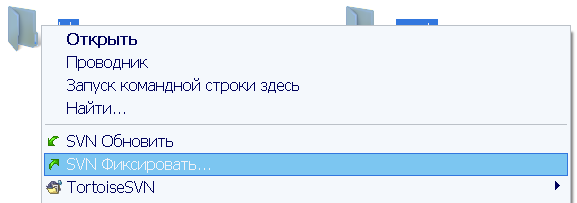
В RabbitVCS (GNU/Linux):
В TortoiseSVN (Windows):
Теперь в веб-интерфейсе проекта на вкладке Source > Browse можно наблюдать появление новой ревизии и состояние проекта, ей соответствующее. При этом вы имеете возможность просмотреть и предыдущие ревизии, а если понадобиться - получить их на свой компьютер.
[править] Задача 1.2 Получить задание к лабораторной работе 1, разобрать на примере RC-цепи
Тема первой лабораторной - моделирование методом несущей на примере электрических цепей. В рамках домашней подготовки от студентов требуется формализовать постановку задачи (объект, его границы при моделировании, цель исследования), записать математическую модель, предложить тестовое воздействие, составить блок-схему программы модели.
В рамках практического задания предлагается разобрать подготовку к лабораторной работе на примере примере RC-цепи.
Файлы модели хранить в каталоге praxis/1. Сделать несколько коммитов во время и по завершению работы.
[править] Занятие 2
Тема занятия: Доплеровский сдвиг навигационного сигнала. Описание сигналов антенной решетки.
Цели занятия:
- развить навыки моделирования: использование векторов, цикл по времени, обработка результатов моделирование, построение графиков и гистограмм.
[править] Задача 2.1 Расчет доплеровского сдвига навигационного сигнала
Постановка задачи:
Автомобильный навигатор является классическим радиоприемным устройством класса аппаратура потребителей спутниковых радионавигационных систем. В процессе своей работы он принимает сигналы от навигационных спутников, оценивает их параметры, выделяет навигационное сообщение, заложенное в сигналах, и, в итоге, решает навигационную задачу - определяет своё местоположение.
Так как навигационные спутники относительно планеты находятся в постоянном движении, да и из-за движения потребителя, возникает эффект Доплера - происходит смещение частоты принимаемого сигнала от номинала. Интересно, в каких пределах может находиться это смещение для неподвижного приемника? Какова гистограмма возможных значений?
Комментарии:
Связь доплеровского сдвига и скорости по линии визирования известна каждому радиотехнику:
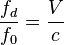 .
.
Несущая частота 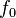 радионавигационного сигнала известна, задается ИКД. Скорость света
радионавигационного сигнала известна, задается ИКД. Скорость света  - фундаментальная константа. Остается определить скорость по линии визирования
- фундаментальная константа. Остается определить скорость по линии визирования 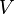 .
.
Потребитель по условию задачи неподвижен. Тогда скорость по линии визирования - проекция вектора скорости спутника на линию визирования. Итого, достаточно определить два вектора - орт от спутника к потребителю и вектор скорости спутника.
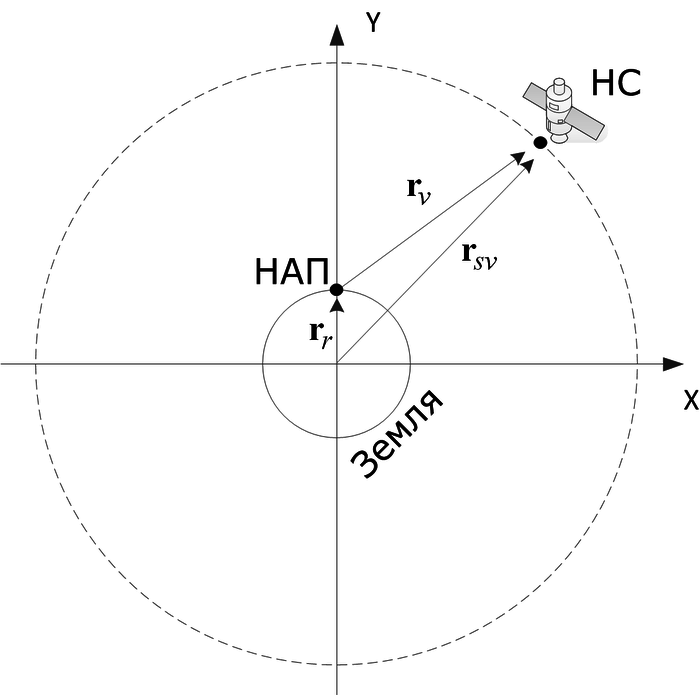
Для простоты ограничимся "плоской" задачей - когда потребитель попадает на подспутниковую траекторию, угловым вращением Земли так же пренебрежем. Иллюстрация - на рисунке:
Выберем СК XOY в которой потребитель расположен на оси OY, его радиус-вектор 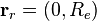 , где
, где 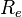 - радиус Земли (учет высоты над уровнем моря для Москвы, 170-190 м, слабо повлияет на результат).
- радиус Земли (учет высоты над уровнем моря для Москвы, 170-190 м, слабо повлияет на результат).
Если определим вектор спутника 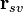 на любой момент витка, то задача будет почти решена, останется:
на любой момент витка, то задача будет почти решена, останется:
- выбрать те положения, для которых y-координата спутника больше y-координаты потребителя (условие видимости),
- по приращению координат определить вектор скорости спутника
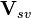 ,
,
- вычитанием найти вектор потребитель-спутник
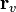 задающий линию визирования,
задающий линию визирования,
- определить скорость сближения по линии визирования
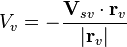 ,
,
- пересчитать скорость сближения в доплеровский сдвиг.
Определить же радиус-вектор спутника легко. Его длина известна, а скорость вращения - примерно оборот за 12 часов (у нас плоская задача, в которой мы пренебрегли различием ECEF и ECI).
Дальше - дело техники.
Шаги по усложнению модели, если результат неубедителен:
- учесть вращение Земли (наклонение орбит известно из ИКД),
- учесть случаи, когда потребитель не попадает под подспутниковую траекторию.
[править] Занятие 3
Тема занятия: Описание сигналов антенной решетки.
Цели занятия:
- привести пример использования метода комплексных амплитуд;
- изложить методику расчет диаграммы направленности антенной решетки, востребованную при подготовке ко второй лабораторной работе;
- освоить создание и использование собственных функций в MATLAB;
- освоить матричные операции;
- научиться визуализировать поверхности.
[править] Задача 3.1 Сигналы и диаграмма направленности антенной решетки
Постановка задачи: Сигнал, приходящий из дальней зоны, принимается системой пространственно разнесенных антенн - антенной решеткой. Размеры антенной решетки значительно меньше постоянной времени корреляции принимаемых сигналов (огибающая, в первом приближении, совпадает для сигналов разных антенн).
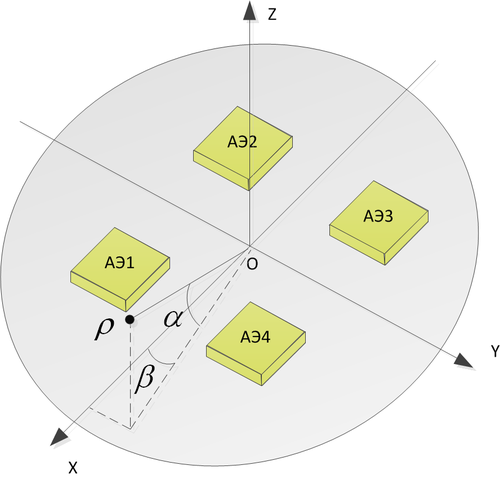
Конфигурация антенной решетки - четырехэлементная, с расположением антенных элементов в углах квадрата со стороной, равной половине длине волны.
Построить серию диаграмм направленности при фокусировке в различных направлениях (зенит, отклонение в сторону на 10, 30, 45, 60 градусов).
Комментарии:
Сигналы антенных элементов
Каждая m-я антенна формирует на выходе свой собственный сигнал 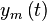 . При фокусировке производят весовое сложение сигналов различных антенн, получая из нескольких сигналов один.
. При фокусировке производят весовое сложение сигналов различных антенн, получая из нескольких сигналов один.
По условию задачи можно пренебречь разностью огибающей для различных точек апертуры антенны. Для ряда практических задач это допущение прекрасно выполняется. Тогда сигналы антенн отличаются только фазой несущей, их математическая модель может быть представлена в виде:
где 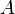 - амплитуда сигналов,
- амплитуда сигналов, 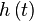 - огибающая,
- огибающая, 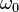 - несущая частота,
- несущая частота, 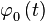 - фаза в начале антенной системы координат OXYZ,
- фаза в начале антенной системы координат OXYZ, 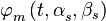 - фазовый набег относительно фазы в начале антенной системы координат для m-й антенны,
- фазовый набег относительно фазы в начале антенной системы координат для m-й антенны,  - угол места и азимут направления на источник сигнала.
- угол места и азимут направления на источник сигнала.
В рамках этой задачи удобно применить метод комплексных амплитуд. Тогда модели сигналов преобразуются к виду
![y_{m}^{{}}\left( t \right)= Ah\left( t \right)\operatorname{Re}\left[ e_{{}}^{i\left( \omega _{0}^{{}}t+\varphi _{0}^{{}}\left( t \right) \right)}e_{{}}^{i\varphi _{m}^{{}}\left( t, \alpha _{s}^{{}},\beta _{s} \right)} \right]](/images/math/b/1/2/b1235c5aa0b5d51f3632f800e880fe08.png) ,
,
обозначим
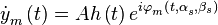 - комплексная амплитуда сигнала m-ой антенны.
- комплексная амплитуда сигнала m-ой антенны.
Составим вектор из комплексных амплитуд сигналов различных антенн
Вектор комплексных амплитуд при приеме образуется после гетеродинирования сигналов (в передающих устройствах последовательность обратная).
Связь фазовых набегов с направлением на источник сигнала
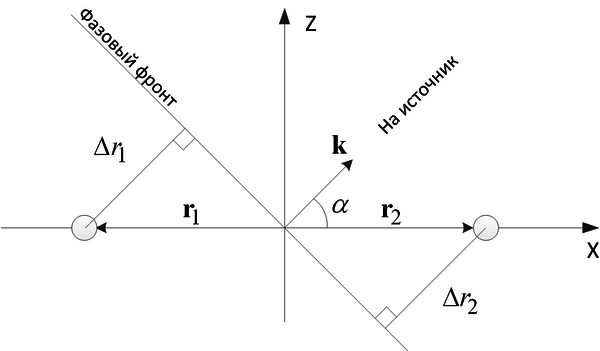
Фазовый набег относительно фазы в начале антенной системы координат определяется положением антенного элемента и направлением прихода сигнала. Его легко рассчитать зная орт 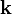 на источник и радиус-вектор
на источник и радиус-вектор  антенного элемента.
антенного элемента.
Разность хода фазового фронта сигнала 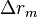 есть скалярное произведение орта и радиус-вектора точки пространства
есть скалярное произведение орта и радиус-вектора точки пространства
фазовый набег связан с разностью хода фазового фронта через длину волны несущей сигнала
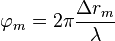 .
.
Для m-oй антенны и направления 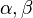 получаем выражение
получаем выражение
Алгоритм фокусировки
При фокусировке антенны в направлении углов  производится умножение вектора-строки фокусировки на вектор-столбец комплексных сигналов
производится умножение вектора-строки фокусировки на вектор-столбец комплексных сигналов
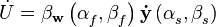 .
.
Вектор фокусировки определяется ожидаемыми фазовыми набегами для направления фокусировки
Диаграмма направленности
Характеристикой направленности называют зависимость нормированной комплексной амплитуды
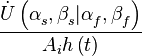 на выходе системы пространственной обработки от направления прихода пробного сигнала
на выходе системы пространственной обработки от направления прихода пробного сигнала  при заданном направлении фокусировки
при заданном направлении фокусировки  . Здесь
. Здесь 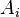 - амплитуда одного сигнала на выходе всенаправленной антенны.
- амплитуда одного сигнала на выходе всенаправленной антенны.
Функция
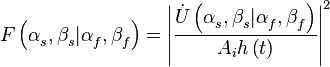 называется диаграммой направленности.
называется диаграммой направленности.
Для принятой модели сигналов диаграмма направленности определяется выражением:
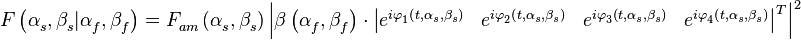 ,
,
где 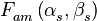 - диаграмма направленности одного антенного элемента.
- диаграмма направленности одного антенного элемента.
Вывод диаграммы направленности в трехмерном виде
Результатом вычислений диаграммы направленности является массив значений 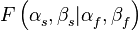 для угла
для угла 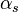 от -180 до 180 градусов,
от -180 до 180 градусов, 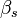 от -90 до 90 (данный выбор диапазона углов не соответствует традиционному определению сферических координат, зато удобен для вывода диаграммы направленности):
от -90 до 90 (данный выбор диапазона углов не соответствует традиционному определению сферических координат, зато удобен для вывода диаграммы направленности):
beta = deg2rad(-90:2:90);
...
F
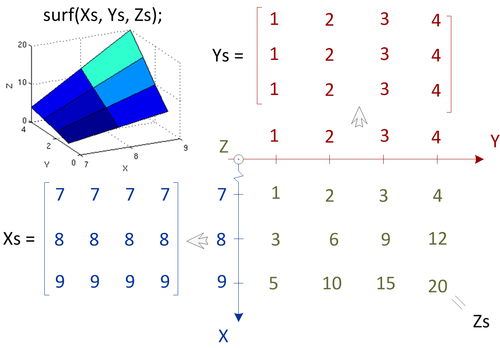
Для задания поверхности недостаточно задать массивы координат её точек, т.к. нужна информация о том, какие точки являются соседними - что с чем соединять. Поэтому в MATLAB используются не три вектора координат, а три матрицы, задающие сетку параметров.
Для "растягивания" векторов координат абсцисс и ординат используется функция meshgrid
Значения 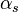 ,
, 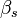 ,
, 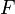 задают три координаты в сферической системе координат. В MATLAB доступны функции построения поверхностей в прямоугольной декартовой системе координат, поэтому перед построением необходимо произвести соответствующее преобразование. Для преобразования из сферической в прямоугольную систему существует функция
задают три координаты в сферической системе координат. В MATLAB доступны функции построения поверхностей в прямоугольной декартовой системе координат, поэтому перед построением необходимо произвести соответствующее преобразование. Для преобразования из сферической в прямоугольную систему существует функция [x, y, z] = sph2cart(beta_m, alpha_m, F), производящая отображение:
y = F .* cos(alpha_m) .* sin(beta_m);
z = F .* sin(alpha_m);
Для вывода поверхности используется функция surf(x, y, z)
surf(x, y, z);
xlabel('x'); ylabel('y'); zlabel('z');
Для лучшего восприятия следует сделать равные пределы по всем трем осям
maxc = max( [max(max(x)) max(max(y)) max(max(z))] );
xlim([minc maxc]); ylim([minc maxc]); zlim([minc maxc]);
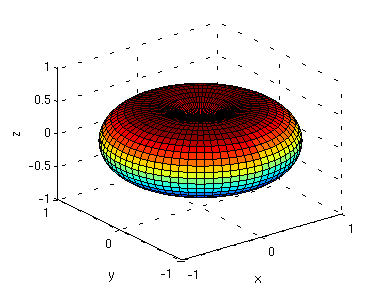
Например, для четвертьволнового вибратора
вывод диаграммы направленности