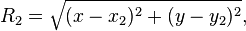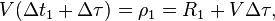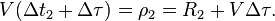Методы навигационных определений (ОП СРНС, лекция) — различия между версиями
Korogodin (обсуждение | вклад) (Новая страница: «== Методы навигационных определений == Назначение навигационной системы - определение коо...») |
Korogodin (обсуждение | вклад) (→Определение угловой ориентации) |
||
| (не показана 31 промежуточная версия 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | == Методы | + | {{ambox |
| + | |mini = 1 | ||
| + | |type = notice | ||
| + | |text = '''Презентация''' | ||
| + | |text-small = [[media:ОП_СРНС-2.pdf|В формате pdf]]<br>[[media:ОП_СРНС-2.ppt|В формате ppt]] | ||
| + | }} | ||
| + | |||
| + | {{ambox | ||
| + | |mini = 1 | ||
| + | |type = notice | ||
| + | |text = '''Время''' | ||
| + | |text-small = 20 минут на контрольные вопросы предыдущего занятия, 105 минут на материал; есть время рассказать про GDOP | ||
| + | }} | ||
| + | |||
| + | :''Предыдущая лекция: [[Введение в СРНС (ОП СРНС, лекция)|Введение в СРНС]]'' | ||
| + | |||
| + | {{ambox | ||
| + | |type = notice | ||
| + | |text = '''ToDo''' | ||
| + | |text-small = * Рассказать про GDOP <br> * Ввести шаблон о занятии, указывать примерное время <br> * Исправить презентацию (добавить картинку по псевдодальномерному методу, заголовок псевдо разностно-дальномерному) | ||
| + | }} | ||
| + | |||
| + | == Методы счисления пути и методы поверхностей положения == | ||
Назначение навигационной системы - определение координат, скорости, ориентации объекта-носителя, а так же обеспечение его шкалой времени. Рассмотрим основные методы решения поставленных задач. | Назначение навигационной системы - определение координат, скорости, ориентации объекта-носителя, а так же обеспечение его шкалой времени. Рассмотрим основные методы решения поставленных задач. | ||
| − | Все методы навигационных определений можно разбить на две большие группы. Традиционно они называются методы счисления пути и методы поверхностей положения. Изложенные ниже подходы справедливы не только для определения координат, но и для оценки остальных навигационных параметров | + | [[file:20121122_Methods.png|center]] |
| + | |||
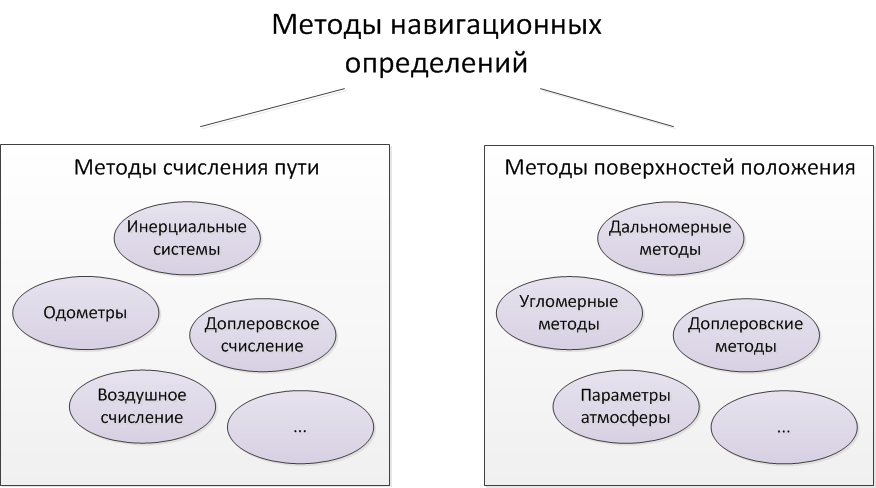
| + | Все методы навигационных определений можно разбить на две большие группы. Традиционно они называются - методы счисления пути и методы поверхностей положения. Изложенные ниже подходы справедливы не только для определения координат, но и для оценки остальных навигационных параметров, но для простоты и наглядности ограничимся примерами определения пространственных координат. | ||
=== Методы счисления пути === | === Методы счисления пути === | ||
| − | При использовании методов счисления пути для решения навигационных задач используются датчики, измеряющие производные от навигационных параметров. Пусть есть некоторый начальный момент времени, в который навигационные параметры, в частности координаты, известны. Для примера рассмотрим задачу | + | При использовании методов счисления пути для решения навигационных задач используются датчики, измеряющие производные от навигационных параметров. Пусть есть некоторый начальный момент времени, в который навигационные параметры, в частности координаты, известны. Интегрируя измерения производных координат (скорости, ускорения, рывка и т.д.) из начальной точки получают измерения самих координат. |
| + | |||
| + | [[file:20121122 S4islenie.png|center]] | ||
| + | |||
| + | Для примера рассмотрим двумерную задачу - определение координат автомобиля. Пусть нам известно положение и скорость в начальный момент времени. Инерциальные датчики, установленные в автомобиле, измеряют три компоненты вектора ускорения его центра масс. Интегрируя оценки ускорения можно получать оценки вектора скорости в каждый момент времени. Интегрируя оценки скорости - получать оценки координат. | ||
| + | |||
| + | Методы счисления пути непосредственно в СРНС не используются. Тем не менее, существует класс комплексированной навигационной аппаратуры потребителей. В комплексированной НАП используются дополнительные источники информации, которые могут помочь улучшить навигационное решение. Наиболее часто встречаемый пример комплексирования - совмещение НАП СРНС и инерциальных датчиков. Такая система использует преимущества спутниковой навигации и инерциальной, нивелируя их недостатки. | ||
| + | |||
| + | === Методы поверхностей положения === | ||
| + | |||
| + | [[file:176398_sphere.png|center]] | ||
| + | |||
| + | К методам поверхностей положения относят различные радиотехнические, астрономические, магнитные, изобарические и другие методы навигации. Эти методы основаны на геометрических свойствах пространства и находящихся в нём полей. При применении методов поверхностей положения измерения ограничивают множество всех возможных положений объекта до некоторой поверхности, откуда и следует название этой группы методов. Если проводятся несколько измерений, то множество возможных положений сокращается до пересечения возможных множеств каждого измерения. Таким образом, ряд измерений может сократить число возможных положений до одной точки - которая и будет оценкой положения. | ||
| + | |||
| + | Во всех [[СРНС]] используются методы поверхностей положения. Основа [[СРНС]] второго поколения - это псевдодальномерный метод навигационных определений. | ||
| + | |||
| + | == Методы навигационных определений, используемые в СРНС второго поколения == | ||
| + | |||
| + | === Дальномерный метод === | ||
| + | |||
| + | Дальномерный метод навигационных определений - это метод определения положения потребителя по измерениям расстояния до нескольких реперных точек с известными координатами. В СРНС он непосредственно не используется, но важен для понимания принципов работы псевдодальномерного метода. | ||
| + | |||
| + | [[file:20121122_mayak1.png|center]] | ||
| + | |||
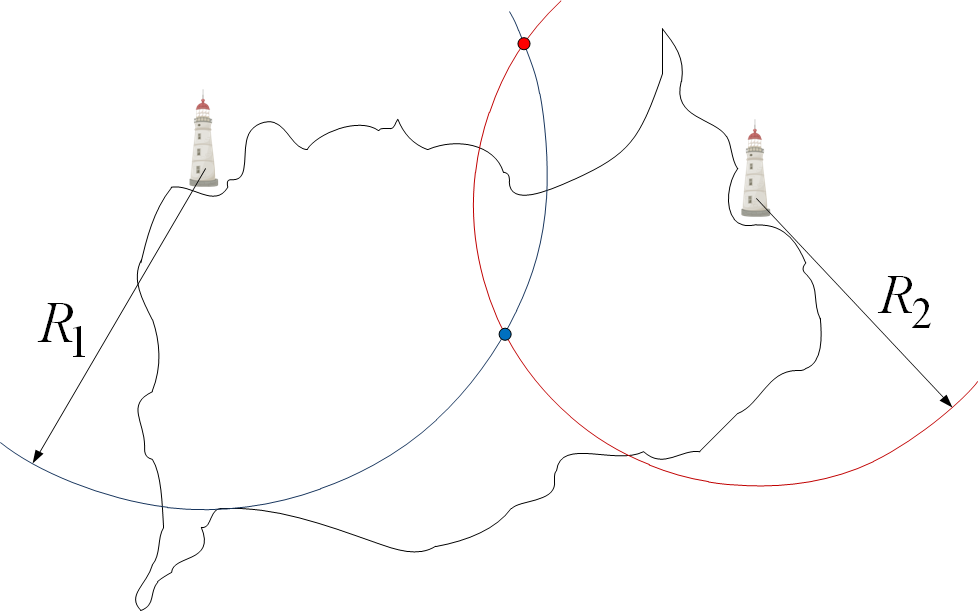
| + | Поясним суть дальномерного метода на примере. Представим, что потребитель - это корабль в море, которому для продолжения плавания требуется узнать где же он расположен. На корабле есть часы, по которым матросы узнают время. На берегу добрые и изобретательные люди установили два маяка, как показано на рисунке. | ||
| + | |||
| + | Капитан предварительно договорился со смотрителем первого маяка, что ровно в полночь, и не наносекундой позже, тот подаст сигнал. Около полуночи матросы собрались вокруг корабельных часов, и как только получили сигнал - записали показания часов. На часах, естественно, было немного за полночь. Скажем, на <math>\Delta t_1</math>. Если известна скорость распространения сигнала <math>V</math>, то сразу можно сказать, что расстояние между первым маяком и кораблем составляет <math>R_1 = V \Delta t_1</math>. Тогда штурман может взять карту, циркуль и начертить окружность радиусом <math>R_1</math> вокруг первого маяка. | ||
| + | |||
| + | [[file:20121122_mayak2.png|center]] | ||
| + | |||
| + | Уравнение этой окружности можно записать как: | ||
| + | :<math>R_1 = \sqrt{(x - x_1)^2 + (y - y_1)^2},</math> | ||
| + | |||
| + | где <math>(x_1, y_1)</math> - координаты первого маяка. | ||
| + | |||
| + | В любой из точек окружности, что попали в море, может находиться корабль. Это уже лучше, чем полная неопределенность, но хотелось бы ограничиться одной возможной точкой. Для этого необходимо повторить измерения расстояния до второго маяка - получить оценку <math>R_2 = V \Delta t_2</math>. Множество возможных положений, при которых расстояние до второго маяка составляет <math>R_2</math> - ещё одна окружность. Её уравнение дополняет первое: | ||
| + | :<math>R_2 = \sqrt{(x - x_2)^2 + (y - y_2)^2}, </math> | ||
| + | |||
| + | где <math>(x_2, y_2)</math> - координаты второго маяка. | ||
| + | |||
| + | [[file:20121122_mayak3.png|center]] | ||
| + | |||
| + | Наш корабль должен одновременно находиться и на одной, и на другой окружности. Таких точек, а это точки пересечения окружностей, всего две. Но одна из них находится на суше, а морякам достаточно выглянуть за борт, чтобы понять, что они всё же в море. Остается один претендент - точка в море, которая и есть измеренное положение корабля. | ||
| + | |||
| + | <div style="background:#ffffff; border:1px dotted #8bcbff; padding:10px; margin-top:10px"> | ||
| + | '''Задача'''<br> | ||
| + | Предположим, что в качестве сигнала использовалась вспышка света, а расстояние до первого маяка составляет 1000 км. Что показали часы в первый раз? | ||
| + | </div> | ||
| + | |||
| + | <div style="background:#ffffff; border:1px dotted #8bcbff; padding:10px; margin-top:10px"> | ||
| + | '''Задача'''<br> | ||
| + | Допустим, часы на корабле запаздывают на 1 мс. Оцените вызванную этим фактом погрешность определения координат. | ||
| + | </div> | ||
| + | |||
| + | === Псевдодальномерный метод === | ||
| + | |||
| + | Ранее мы считали, что часы на корабле и маяках синхронизированы. Для реальных часов это нехарактерно. Пусть часы на корабле опережают часы маяков на величину <math>\Delta\tau</math>. Тогда часы моряков будут измерять задержку сигнала со смещением на <math>\Delta\tau</math>, таким образом вместо расстояний измерять величины: | ||
| + | :<math>V(\Delta t_1 + \Delta \tau) = \rho_1 = R_1 + V\Delta\tau,</math> | ||
| + | :<math>V(\Delta t_2 + \Delta \tau) = \rho_2 = R_2 + V\Delta\tau.</math> | ||
| + | |||
| + | Величины <math>\rho</math> называются ''псевдодальностями''. | ||
| + | |||
| + | <div style="background:#ffffff; border:1px dotted #8bcbff; padding:10px; margin-top:10px"> | ||
| + | '''Задача'''<br> | ||
| + | Запишите уравнения, связывающие псевдодальности, координаты маяков и координаты корабля. Сколько неизвестных в полученной системе уравнений? Каков их "физический смысл"? Сколько маяков необходимо использовать для решения задачи? | ||
| + | </div> | ||
| + | |||
| + | Псевдодальномерный метод используется и в СРНС. Спутники выступают в качестве сети синхронизированных маяков. При этом маяки хоть и перемещаются в пространстве с огромной скоростью, навигационная аппаратура с помощью передаваемых эфемерид рассчитывает положение спутников на момент излучения. Как и в примере с кораблем, для определения координат на плоскости достаточно трех спутников. Для получения трех пространственных координат потребуется дополнительное измерение псевдодальности до четвертого космического аппарата. | ||
| + | |||
| + | |||
| + | === Псевдо радиально-скоростной метод === | ||
| + | |||
| + | [[file:20121122_Dopler.png|center]] | ||
| + | |||
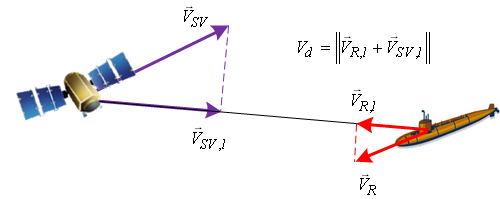
| + | Ранее мы рассмотрели задачу определения координат потребителя и поправки к его шкале времени. Аналогично решается задача определения скорости потребителя. Отличие заключается в том, что входными данными задачи выступают смещенные оценки взаимной скорости, а не расстояния. Смещение определяется скоростью расхождения часов потребителя и спутников. | ||
| + | |||
| + | Благодаря эффекту Доплера взаимная скорость пропорциональная доплеровскому сдвигу частоты, оценку которого производит приемник. | ||
| + | |||
| + | === Определение угловой ориентации === | ||
| + | |||
| + | [[file:20121122_Uglomer.png|center]] | ||
| + | |||
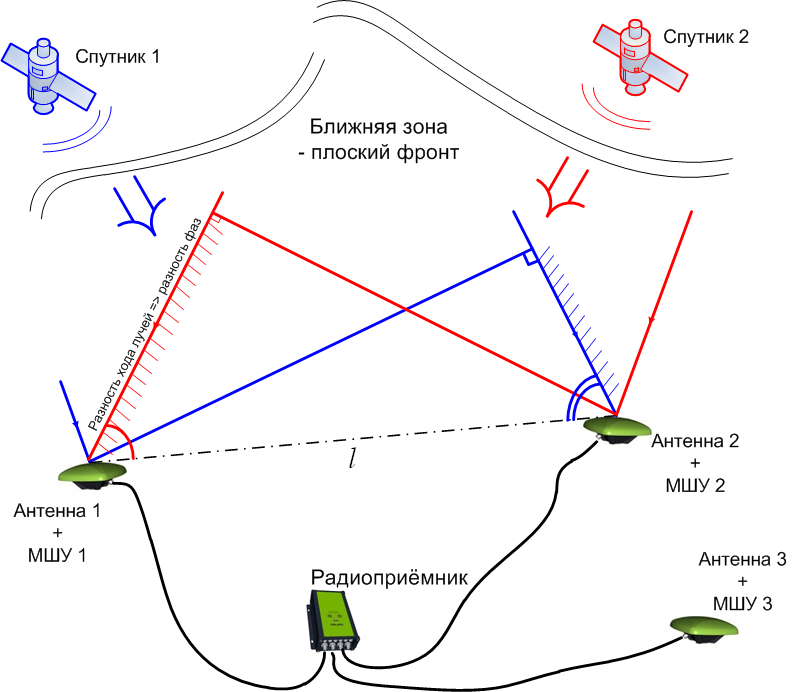
| + | Угловая ориентация потребителя определяется путем сравнения задержек сигнала в нескольких разнесенных в пространстве точках. Разность хода сигнала при этом связана с углом между линией, соединяющей антенны, и направлением на спутник. Проведя измерения для нескольких спутников можно получить единственное решение для параметров ориентации антенной системы. | ||
| − | + | [[file:20130913_ynap.gif|center]] | |
| − | + | == Литература == | |
| − | + | * {{Публикация:Перов_2010_ГЛОНАСС}}: | |
| + | :§4.1, §4.2, §4.3, §4.5, §4.6. | ||
| − | + | == Контрольные вопросы == | |
| − | + | 1. Какие методы определения координат, скорости, времени и ориентации Вам известны? Какие измерения необходимо провести для их реализации? | |
[[Категория: ОП СРНС (дисциплина)]] | [[Категория: ОП СРНС (дисциплина)]] | ||
Текущая версия на 12:00, 13 сентября 2013
| Презентация |
| Время 20 минут на контрольные вопросы предыдущего занятия, 105 минут на материал; есть время рассказать про GDOP
|
- Предыдущая лекция: Введение в СРНС
| ToDo * Рассказать про GDOP
* Ввести шаблон о занятии, указывать примерное время * Исправить презентацию (добавить картинку по псевдодальномерному методу, заголовок псевдо разностно-дальномерному) |
Содержание |
[править] Методы счисления пути и методы поверхностей положения
Назначение навигационной системы - определение координат, скорости, ориентации объекта-носителя, а так же обеспечение его шкалой времени. Рассмотрим основные методы решения поставленных задач.
Все методы навигационных определений можно разбить на две большие группы. Традиционно они называются - методы счисления пути и методы поверхностей положения. Изложенные ниже подходы справедливы не только для определения координат, но и для оценки остальных навигационных параметров, но для простоты и наглядности ограничимся примерами определения пространственных координат.
[править] Методы счисления пути
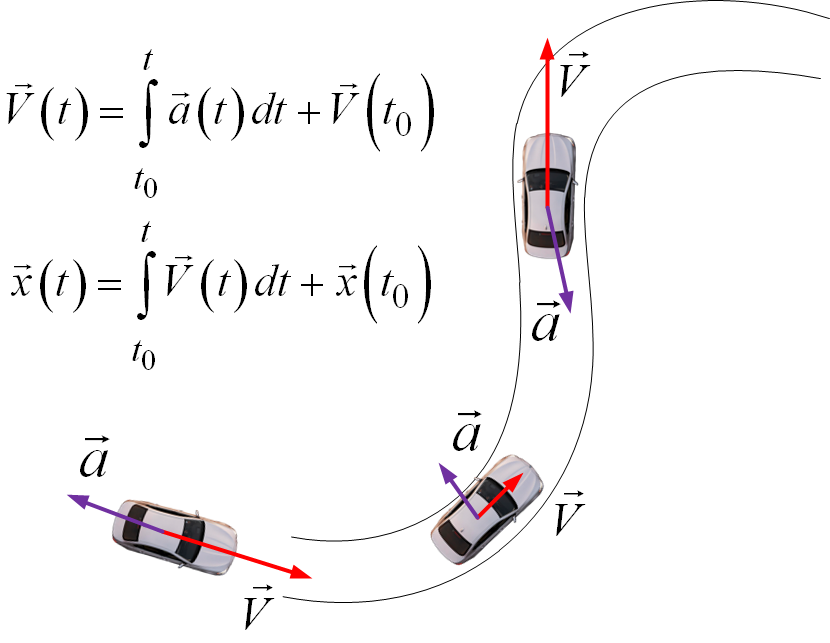
При использовании методов счисления пути для решения навигационных задач используются датчики, измеряющие производные от навигационных параметров. Пусть есть некоторый начальный момент времени, в который навигационные параметры, в частности координаты, известны. Интегрируя измерения производных координат (скорости, ускорения, рывка и т.д.) из начальной точки получают измерения самих координат.
Для примера рассмотрим двумерную задачу - определение координат автомобиля. Пусть нам известно положение и скорость в начальный момент времени. Инерциальные датчики, установленные в автомобиле, измеряют три компоненты вектора ускорения его центра масс. Интегрируя оценки ускорения можно получать оценки вектора скорости в каждый момент времени. Интегрируя оценки скорости - получать оценки координат.
Методы счисления пути непосредственно в СРНС не используются. Тем не менее, существует класс комплексированной навигационной аппаратуры потребителей. В комплексированной НАП используются дополнительные источники информации, которые могут помочь улучшить навигационное решение. Наиболее часто встречаемый пример комплексирования - совмещение НАП СРНС и инерциальных датчиков. Такая система использует преимущества спутниковой навигации и инерциальной, нивелируя их недостатки.
[править] Методы поверхностей положения
К методам поверхностей положения относят различные радиотехнические, астрономические, магнитные, изобарические и другие методы навигации. Эти методы основаны на геометрических свойствах пространства и находящихся в нём полей. При применении методов поверхностей положения измерения ограничивают множество всех возможных положений объекта до некоторой поверхности, откуда и следует название этой группы методов. Если проводятся несколько измерений, то множество возможных положений сокращается до пересечения возможных множеств каждого измерения. Таким образом, ряд измерений может сократить число возможных положений до одной точки - которая и будет оценкой положения.
Во всех СРНС используются методы поверхностей положения. Основа СРНС второго поколения - это псевдодальномерный метод навигационных определений.
[править] Методы навигационных определений, используемые в СРНС второго поколения
[править] Дальномерный метод
Дальномерный метод навигационных определений - это метод определения положения потребителя по измерениям расстояния до нескольких реперных точек с известными координатами. В СРНС он непосредственно не используется, но важен для понимания принципов работы псевдодальномерного метода.
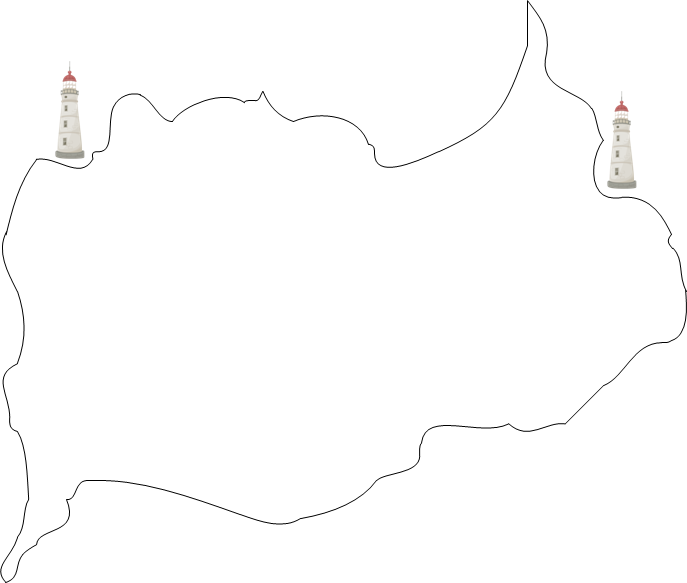
Поясним суть дальномерного метода на примере. Представим, что потребитель - это корабль в море, которому для продолжения плавания требуется узнать где же он расположен. На корабле есть часы, по которым матросы узнают время. На берегу добрые и изобретательные люди установили два маяка, как показано на рисунке.
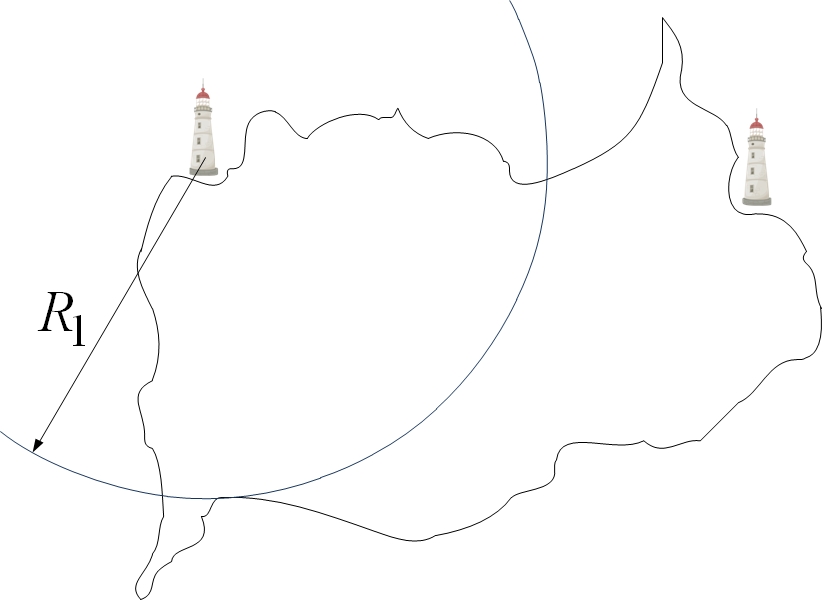
Капитан предварительно договорился со смотрителем первого маяка, что ровно в полночь, и не наносекундой позже, тот подаст сигнал. Около полуночи матросы собрались вокруг корабельных часов, и как только получили сигнал - записали показания часов. На часах, естественно, было немного за полночь. Скажем, на 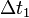 . Если известна скорость распространения сигнала
. Если известна скорость распространения сигнала 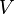 , то сразу можно сказать, что расстояние между первым маяком и кораблем составляет
, то сразу можно сказать, что расстояние между первым маяком и кораблем составляет  . Тогда штурман может взять карту, циркуль и начертить окружность радиусом
. Тогда штурман может взять карту, циркуль и начертить окружность радиусом 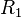 вокруг первого маяка.
вокруг первого маяка.
Уравнение этой окружности можно записать как:
где 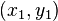 - координаты первого маяка.
- координаты первого маяка.
В любой из точек окружности, что попали в море, может находиться корабль. Это уже лучше, чем полная неопределенность, но хотелось бы ограничиться одной возможной точкой. Для этого необходимо повторить измерения расстояния до второго маяка - получить оценку 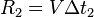 . Множество возможных положений, при которых расстояние до второго маяка составляет
. Множество возможных положений, при которых расстояние до второго маяка составляет 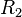 - ещё одна окружность. Её уравнение дополняет первое:
- ещё одна окружность. Её уравнение дополняет первое:
где 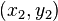 - координаты второго маяка.
- координаты второго маяка.
Наш корабль должен одновременно находиться и на одной, и на другой окружности. Таких точек, а это точки пересечения окружностей, всего две. Но одна из них находится на суше, а морякам достаточно выглянуть за борт, чтобы понять, что они всё же в море. Остается один претендент - точка в море, которая и есть измеренное положение корабля.
Задача
Предположим, что в качестве сигнала использовалась вспышка света, а расстояние до первого маяка составляет 1000 км. Что показали часы в первый раз?
Задача
Допустим, часы на корабле запаздывают на 1 мс. Оцените вызванную этим фактом погрешность определения координат.
[править] Псевдодальномерный метод
Ранее мы считали, что часы на корабле и маяках синхронизированы. Для реальных часов это нехарактерно. Пусть часы на корабле опережают часы маяков на величину  . Тогда часы моряков будут измерять задержку сигнала со смещением на
. Тогда часы моряков будут измерять задержку сигнала со смещением на  , таким образом вместо расстояний измерять величины:
, таким образом вместо расстояний измерять величины:
Величины  называются псевдодальностями.
называются псевдодальностями.
Задача
Запишите уравнения, связывающие псевдодальности, координаты маяков и координаты корабля. Сколько неизвестных в полученной системе уравнений? Каков их "физический смысл"? Сколько маяков необходимо использовать для решения задачи?
Псевдодальномерный метод используется и в СРНС. Спутники выступают в качестве сети синхронизированных маяков. При этом маяки хоть и перемещаются в пространстве с огромной скоростью, навигационная аппаратура с помощью передаваемых эфемерид рассчитывает положение спутников на момент излучения. Как и в примере с кораблем, для определения координат на плоскости достаточно трех спутников. Для получения трех пространственных координат потребуется дополнительное измерение псевдодальности до четвертого космического аппарата.
[править] Псевдо радиально-скоростной метод
Ранее мы рассмотрели задачу определения координат потребителя и поправки к его шкале времени. Аналогично решается задача определения скорости потребителя. Отличие заключается в том, что входными данными задачи выступают смещенные оценки взаимной скорости, а не расстояния. Смещение определяется скоростью расхождения часов потребителя и спутников.
Благодаря эффекту Доплера взаимная скорость пропорциональная доплеровскому сдвигу частоты, оценку которого производит приемник.
[править] Определение угловой ориентации
Угловая ориентация потребителя определяется путем сравнения задержек сигнала в нескольких разнесенных в пространстве точках. Разность хода сигнала при этом связана с углом между линией, соединяющей антенны, и направлением на спутник. Проведя измерения для нескольких спутников можно получить единственное решение для параметров ориентации антенной системы.
[править] Литература
- ГЛОНАСС. Принципы построения и функционирования / Под. ред. Перова А.И., Харисова В.Н.. — изд. 4-е, перераб. и доп.. — М.: Радиотехника, 2010. — 800 с. (подробнее...):
- §4.1, §4.2, §4.3, §4.5, §4.6.
[править] Контрольные вопросы
1. Какие методы определения координат, скорости, времени и ориентации Вам известны? Какие измерения необходимо провести для их реализации?