Пространственные системы координат (ОП СРНС, лекция) — различия между версиями
Korogodin (обсуждение | вклад) (→Топоцентрическая геодезическая система координат) |
Korogodin (обсуждение | вклад) (→Замечания на будущий год) |
||
| (не показана 31 промежуточная версия 1 участника) | |||
| Строка 9: | Строка 9: | ||
Существует значительное многообразие типов систем координат, отличающихся законом связи координат и положения в пространстве. В приложениях СРНС наиболее востребованы системы координат | Существует значительное многообразие типов систем координат, отличающихся законом связи координат и положения в пространстве. В приложениях СРНС наиболее востребованы системы координат | ||
* по геометрии: прямоугольные и эллипсоидальные; | * по геометрии: прямоугольные и эллипсоидальные; | ||
| − | * по масштабу: общеземные, локальные и связанные с объектом; | + | * по масштабу: общеземные, национальные, локальные и связанные с объектом; |
* по движению: инерциальные и неинерциальные. | * по движению: инерциальные и неинерциальные. | ||
| Строка 22: | Строка 22: | ||
=== Декартова система координат, связанная с объектом === | === Декартова система координат, связанная с объектом === | ||
| + | |||
| + | ==== Углы Эйлера ==== | ||
| + | |||
| + | ==== Рысканье, крен, тангаж ==== | ||
=== Геоцентрическая прямоугольная система координат, связанная с Землей === | === Геоцентрическая прямоугольная система координат, связанная с Землей === | ||
| Строка 53: | Строка 57: | ||
==== Датум ==== | ==== Датум ==== | ||
| − | Набор параметров, связывающий ECEF и ENU, называется '''датумом''' или часто просто геодезической системой. | + | Набор параметров, связывающий ECEF и ENU, называется '''датумом''' или часто просто геодезической системой (геодезическая система параметров земли, ГСПЗ). |
При работе с СРНС наиболее часто встречаются: | При работе с СРНС наиболее часто встречаются: | ||
| − | * WGS-84 | + | * WGS-84 - основной датум системы NAVSTAR GPS |
| − | * ПЗ | + | * ПЗ-90 - основной датум системы ГЛОНАСС, в версии ПЗ-90.02 совпадает с WGS-84 с дециметровой точностью, в версии ПЗ-90.11 (основная с 01.01.2014 года) - с сантиметровой. |
| − | * СК-42 | + | * СК-42 (Пулково-1942) - датум, в котором составлены большинство гражданских карт, созданных в Советском Союзе |
| − | * СК-63 | + | * СК-95 - обновленный вариант СК-42 |
| − | * ETRF-00 | + | * СК-63 - аналогичен СК-42, но параметры засекречены, используется в военных приложениях |
| + | * ITRS - "международная земная система координат", продвигаемая Международной ассоциацией геодезии | ||
| + | * ETRF-00 - основной датум системы Галилео. | ||
| + | |||
| + | Для примера, состав ГСПЗ ПЗ-90: | ||
| + | * Фундаментальные геодезические постоянные; | ||
| + | * Параметры общеземного эллипсоида; | ||
| + | * ''Система координат'' ПЗ-90, закрепляемая координатами пунктов Мировой космической геодезической сети (МКГС), находящихся на астрономо-геодезических пунктах Минобороны России; | ||
| + | * Планетарные модели нормального и аномального гравитационного поля Земли; | ||
| + | * Элементы трансформирования между системой координат ПЗ-90, Мировой геодезической системой координат WGS-84, Международной земной системой координат ITRS и национальными референцными системами координат России. | ||
==== Начало СК ==== | ==== Начало СК ==== | ||
| Строка 102: | Строка 115: | ||
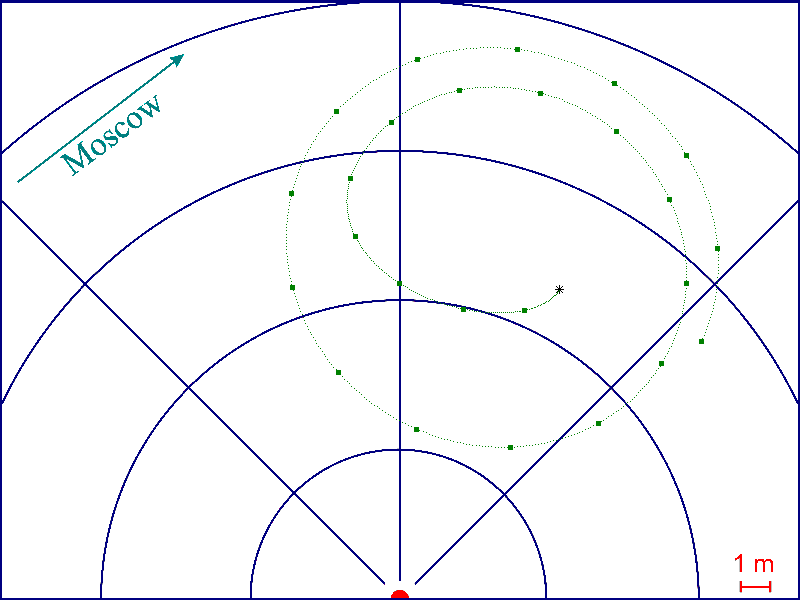
<center>Движение истинного северного полюса (точки с шагом в 30 дней)</center> | <center>Движение истинного северного полюса (точки с шагом в 30 дней)</center> | ||
| − | ==== | + | Положение магнитного и географического полюса отличаются существенно. Например, в последние годы северный магнитный полюс изменяет своё положение со скоростью около 70 км в год. Поэтому, компас показывает направление на север лишь примерно. |
| + | |||
| + | ==== Параметры эллипсоида ==== | ||
'''Геоид''' - фигура сложной формы, образованная поверхностью уровня вод Мирового океана, продолженной под материками. Эта поверхность во всех точках перпендикулярна (нормальна) вектору силы тяжести, при этом эта нормаль, как правило, не проходит через центр тяжести планеты. | '''Геоид''' - фигура сложной формы, образованная поверхностью уровня вод Мирового океана, продолженной под материками. Эта поверхность во всех точках перпендикулярна (нормальна) вектору силы тяжести, при этом эта нормаль, как правило, не проходит через центр тяжести планеты. | ||
| Строка 111: | Строка 126: | ||
'''Эллипсо́ид враще́ния''' (сферо́ид) — это фигура, образованная при вращении эллипса вокруг одной из его осей. | '''Эллипсо́ид враще́ния''' (сферо́ид) — это фигура, образованная при вращении эллипса вокруг одной из его осей. | ||
| + | |||
| + | СК-42 и т.п. основаны на эллипсоиде Красовского (1940), WGS-84 - на эллипсоиде GRS80. | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |-align="center" | ||
| + | ! Эллипсоид | ||
| + | ! Использование | ||
| + | ! Большая полуось, a, м | ||
| + | ! Малая полуось, b, м | ||
| + | ! Сжатие f = (a-b)/a | ||
| + | |||
| + | |- | ||
| + | | Красовского (1940) | ||
| + | | Россия и др.; Пулково-1942 | ||
| + | | 6378245 | ||
| + | | 6356863 | ||
| + | | 1/298,3 | ||
| + | |||
| + | |- | ||
| + | | GRS80 | ||
| + | | международный; WGS84 | ||
| + | | 6378137 | ||
| + | | 6356752,31425 | ||
| + | | 1/298,25722356 | ||
| + | |||
| + | |} | ||
| + | |||
| + | ''Референц-эллипсоид'' | ||
| + | ''Общеземной эллипсоид'' | ||
==== Топоцентрические и геоцентрические геодезические системы координат ==== | ==== Топоцентрические и геоцентрические геодезические системы координат ==== | ||
| Строка 116: | Строка 160: | ||
Геодезические системы координат можно разделить на ''геоцентрические'' (общеземные, глобальные) и ''топоцентрические (национальные)''. | Геодезические системы координат можно разделить на ''геоцентрические'' (общеземные, глобальные) и ''топоцентрические (национальные)''. | ||
| − | Глобальные системы координат минимизируют разницу между геоидом и | + | Глобальные системы координат минимизируют разницу между геоидом и эллипсоидом по всей поверхности Земли или большей её части, при этом: |
*объем эллипсоида предполагается равным объему геоида; | *объем эллипсоида предполагается равным объему геоида; | ||
*большая полуось эллипсоида лежит в плоскости экватора геоида; | *большая полуось эллипсоида лежит в плоскости экватора геоида; | ||
*малая полуось направлена по оси вращения Земли. | *малая полуось направлена по оси вращения Земли. | ||
| + | Примеры систем - ПЗ-90, WGS-84. | ||
| − | В топоцентрической (национальной) | + | В топоцентрической (национальной) эллипсоид располагают так, чтобы для заданной территории среднеквадратичное отклонение поверхности эллипсоида от поверхности геоида было минимальным. Отклонения на другой стороне Земли при этом может быть сколь угодно велико. Центр референц-эллипсоида может оказаться значительно смещенным от центра масс Земли. Примеры национальных систем - СК-42, СК-95. |
| + | |||
| + | ==== Картографические проекции ==== | ||
=== Геоцентрическая инерциальная система координат === | === Геоцентрическая инерциальная система координат === | ||
| Строка 128: | Строка 175: | ||
Любая система координат, которая жестко связана с Землей, существенно отлична от инерционной в масштабах движения космических аппаратов. Примерно за сутки эта система координат успевает развернуться относительно инерционных. | Любая система координат, которая жестко связана с Землей, существенно отлична от инерционной в масштабах движения космических аппаратов. Примерно за сутки эта система координат успевает развернуться относительно инерционных. | ||
| + | |||
| + | Геоцентрическая инерциальная система координат <math>OX_0Y_0Z_0</math>, в первом приближении, не изменяет своей ориентации относительно инерциального пространства. Плоскость <math>X_0OY_0</math> лежит в плоскости экватора Земли, ось <math>OX_0</math> направлена в точку весеннего равноденствия - точку Весны или точку Овна <math>\gamma</math>, которая лежит на линии пересечения плоскости экватора Земли и плоскости орбитального движение Земли вокруг Солнца. Ось <math>OZ_0</math> дополняет прямоугольную систему координат до правой, т.е. направлена вдоль оси вращения Земли в сторону Северного полюса. | ||
== Преобразование координат == | == Преобразование координат == | ||
| Строка 135: | Строка 184: | ||
=== Преобразование координат прямоугольных систем в геоцентрические === | === Преобразование координат прямоугольных систем в геоцентрические === | ||
| − | === | + | === Преобразование геодезических систем координат различных датумов === |
| + | |||
| + | Есть различные подходы и преобразования, в основном основанные на пересчете в прямоугольные СК. | ||
| + | |||
| + | Например, СК-42 и WGS-84 связаны как (расчет на основании преобразования Молоденского): | ||
| + | {| class="wikitable" border="1" | ||
| + | |-align="center" | ||
| + | ! Направление | ||
| + | ! dX, м | ||
| + | ! dY, м | ||
| + | ! dZ, м | ||
| + | ! da, м | ||
| + | ! df, | ||
| + | |||
| + | |- | ||
| + | | Из СГ-42 в WGS-84 | ||
| + | | +28.0 | ||
| + | | -130.0 | ||
| + | | -95.0 | ||
| + | | -108.0 | ||
| + | | +0.00480795 | ||
| + | |||
| + | |} | ||
| + | |||
| + | == Литература == | ||
| + | |||
| + | #{{Публикация:Перов 2010 ГЛОНАСС}} : Глава 3, параграф 3.1 | ||
| + | #{{Публикация:Перов 2012 Основы построения спутниковых радионавигационных систем}} : Глава 2, параграф 2.1 | ||
| + | |||
| + | == Замечания на будущий год == | ||
| + | |||
| + | Лекция разбилась на полторы пары. Первое полупарие обсуждали: | ||
| + | * Понятие системы координат | ||
| + | * Классификация СК по различным признакам | ||
| + | * Понятие декартовой СК | ||
| + | * Локальная СК (наглядный пример - СК аэропорта) | ||
| + | * Локальная СК, связанная с объектом (на примере самолета) | ||
| + | * Углы Эйлера | ||
| + | * Рысканье, крен, тангаж | ||
| + | * Преимущества описания кватернионами | ||
| + | * Матрицы повротов (вывод матрицы на плоскости, обобщение на трехмерный случай). | ||
| + | |||
| + | Второе занятие (одна пара): | ||
| + | * Простенькая задачка на поворот осей (на 90 градусов) | ||
| + | * ECEF | ||
| + | * ECEF можно ввести множество. Нужно определиться с началом отсчета, полюсом и нулевым меридианом. | ||
| + | * Центр тяжести Земли и его эволюция | ||
| + | * Полюс и его эволюция (заодно про несовпадение с магнитным полюсом) | ||
| + | * Гринвич и нулевой меридиан по международному стандарту | ||
| + | * Человек ориентируется больше по поверхности Земли -> Геодезические СК | ||
| + | * Простейший вариант - аппроксимировать сферой в выбранном ECEF. | ||
| + | * Задачка по расчету координат на необитаемом острове | ||
| + | * Сфера не лучшая аппроксимация, Земля всё-таки сплюснута на 20+20 км по полюсам. Отсюда эллипсоидальные геодезические СК. | ||
| + | * Эллипсы бывают разные. Некоторые общеземные (тот, что в WGS), некоторые - местячковые (Красовского). | ||
| + | * Формулы связи ECEF и ENU. | ||
| + | * Следующий уровень аппроксимации - геоид. Особенно востребован у моряков. | ||
| + | * Датум как совокупность. Примеры датумов. Датум, как система, определяемая совокупностью станций наблюдения и математических моделей. Отсюда - расхождение их как функция времени. | ||
| + | * Определились с координатами на сфере. Замечательно. Но пользуемся-то мы плоскими картами. Сферический планшетов нет у нас. Отсюда - картографическая проекция. | ||
| + | * Классификация картографических проекций и их примеры. | ||
| + | * Проекция Меркатора на примере Яндекса. Минус - несохранение масштаба. Плюс - простота проверки курса. | ||
| + | * Первая и вторая геодезические задачи. Решение второй геодезической задачи в сферической проекции Меркатора на примере Яндекса. Предельные случаи. | ||
| + | |||
| + | == Ссылки == | ||
*[http://astro.tsu.ru/TGP/ Т.В. Бордовицына ТЕХНОЛОГИИ ГЛОБАЛЬНОГО ПОЗИЦИОНИРОВАНИЯ (GPS/ГЛОНАСС)] | *[http://astro.tsu.ru/TGP/ Т.В. Бордовицына ТЕХНОЛОГИИ ГЛОБАЛЬНОГО ПОЗИЦИОНИРОВАНИЯ (GPS/ГЛОНАСС)] | ||
| Строка 142: | Строка 253: | ||
*[http://habrahabr.ru/post/143898/ Хабрахабр. Занимательная геодезия] | *[http://habrahabr.ru/post/143898/ Хабрахабр. Занимательная геодезия] | ||
*[http://eqworld.ipmnet.ru/ru/info/sci-edu/Earth_orientation_rus.html Л.Д. Акуленко, С.А. Кумакшев, А.М. Шматков Математический прогноз движения полюса Земли] | *[http://eqworld.ipmnet.ru/ru/info/sci-edu/Earth_orientation_rus.html Л.Д. Акуленко, С.А. Кумакшев, А.М. Шматков Математический прогноз движения полюса Земли] | ||
| + | *[http://kartograph.org/showcase/projections Интерактивное представление различных картографических проекций] | ||
[[Категория: ОП СРНС (дисциплина)]] | [[Категория: ОП СРНС (дисциплина)]] | ||
Текущая версия на 13:51, 2 октября 2013
Конечная функция СРНС - ответить на вопросы "где?" и "когда?" применительно к потребителю. Ответом может послужить и некоторое контекстное описание, но удобнее пользоваться абстракцией координат.
Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Перед СРНС ставится задача определения трех пространственных координат и одной временной (времени). Начнем с изучения различных пространственных систем координат, используемых в СРНС.
Содержание
|
[править] Виды пространственных систем координат
Существует значительное многообразие типов систем координат, отличающихся законом связи координат и положения в пространстве. В приложениях СРНС наиболее востребованы системы координат
- по геометрии: прямоугольные и эллипсоидальные;
- по масштабу: общеземные, национальные, локальные и связанные с объектом;
- по движению: инерциальные и неинерциальные.
[править] Локальная декартова система координат
Декартова система координат - это прямоугольная система координат с равным масштабом по различным осям.
Для определения декартовой системы координат достаточно задать:
- положение начала системы координат
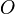 ;
;
- направление осей
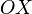 ,
,  ,
, 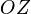 ;
;
- масштаб по осям.
[править] Декартова система координат, связанная с объектом
[править] Углы Эйлера
[править] Рысканье, крен, тангаж
[править] Геоцентрическая прямоугольная система координат, связанная с Землей
Общепризнанное международное название систем координат данного типа - ECEF (Earth Centered, Earth Fixed). Как следует из названия, геоцентрическая неинерциальная система координат 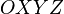 жестко связана с Землей и имеет начало в её центре масс.
жестко связана с Землей и имеет начало в её центре масс.
Ось 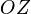 направлена по оси вращения Земли в сторону Северного полюса.
направлена по оси вращения Земли в сторону Северного полюса.
Ось 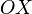 лежит в плоскости земного экватора, связана с нулевым меридианом.
лежит в плоскости земного экватора, связана с нулевым меридианом.
Ось  дополняет систему координат до правой.
дополняет систему координат до правой.
В этой системе координат удобно описывать положение точек, находящихся на земле или движущихся вблизи неё.
ECEF жестко связана с Землей и вращается с ней относительно инерциального пространства. В такой системе положения точек, закрепленных на твердой поверхности Земли, имеют координаты, которые подвергаются только малым изменениям со временем из-за геофизических эффектов. Постоянство координат наземных точек - главное преимущество СК, связанных с Землей.
Существует множество разновидностей ECEF СК, отличающиеся принятым центром масс Земли, нулевым меридианом (об этом далее в разделе про геодезические СК).
[править] Геодезическая система координат
Несмотря на то, что окружающее человека пространство трехмерно, нам удобнее пользоваться двухмерными картами. На то есть ряд причин:
- с двухмерными образами намного удобнее обращаться - создавать, использовать, хранить;
- человек использует не весь объем планеты, а лишь очень тонкую прослойку у поверхности.
Поверхность же эта, в первом приближении, очень близка к сфере. Рисунок дорог, домов, гор, рек и континентов с этой поверхности скопирован на карты.
Находить точку на карте удобнее по абсциссе и ординате на этой карте, а не координатам ECEF. Например, что можно сказать, без дополнительных расчетов, о местоположении точки (4366997, -4867716, 79259)? Или (2701898, -3375560, 4906826)? Где они на карте? На какой высоте расположены? В каком полушарии? Часовом поясе?
Система координат карт - геодезическая. Две координаты задают положение на эллипсоиде, аппроксимирующем земную поверхность, и одна координата - отклонение по высоте от этого эллипсоида (ENU - east, north, up). Но это качественно, а как перейти к конкретным числам?
[править] Датум
Набор параметров, связывающий ECEF и ENU, называется датумом или часто просто геодезической системой (геодезическая система параметров земли, ГСПЗ).
При работе с СРНС наиболее часто встречаются:
- WGS-84 - основной датум системы NAVSTAR GPS
- ПЗ-90 - основной датум системы ГЛОНАСС, в версии ПЗ-90.02 совпадает с WGS-84 с дециметровой точностью, в версии ПЗ-90.11 (основная с 01.01.2014 года) - с сантиметровой.
- СК-42 (Пулково-1942) - датум, в котором составлены большинство гражданских карт, созданных в Советском Союзе
- СК-95 - обновленный вариант СК-42
- СК-63 - аналогичен СК-42, но параметры засекречены, используется в военных приложениях
- ITRS - "международная земная система координат", продвигаемая Международной ассоциацией геодезии
- ETRF-00 - основной датум системы Галилео.
Для примера, состав ГСПЗ ПЗ-90:
- Фундаментальные геодезические постоянные;
- Параметры общеземного эллипсоида;
- Система координат ПЗ-90, закрепляемая координатами пунктов Мировой космической геодезической сети (МКГС), находящихся на астрономо-геодезических пунктах Минобороны России;
- Планетарные модели нормального и аномального гравитационного поля Земли;
- Элементы трансформирования между системой координат ПЗ-90, Мировой геодезической системой координат WGS-84, Международной земной системой координат ITRS и национальными референцными системами координат России.
[править] Начало СК
Первым делом, необходимо определиться с началом системы координат.
Центр масс - центр инерции - геометрическая точка, положение которой характеризует распределение масс в теле или механической системе.
Центр масс Земли, или геоцентр, используется в качестве начала во многих системах координат, т.к. он значительно более стабилен, чем точки поверхности земли. Определяется геоцентр по наблюдению спутников, движущихся в гравитационном поле Земли. Учитывает он массу не только твердых пород, но и океанов, атмосферы.
Анализ спутниковых лазерных дальномерных наблюдений уверенно показывает, что система отсчета, реализованная в координатах станций наблюдений, неподвижных относительно земной коры, ощутимо смещается относительно центра масс Земли. Так, например, в России используется Балтийская система высот - система абсолютных высот, отсчёт которых ведётся от нуля кронштадтского футштока. Высоты на картах отмечены относительного этого футштока. Но он изменяет свою высоту вместе со смещением тектонических плит, а вместе с ним смещаются и отечественные карты относительно карт, составленных, скажем, в США.
На основании современных геофизических моделей и результатов обработки лазерных измерений, GPS и DORIS сделан вывод, что величина скоростей вековых движений (тренд) геоцентра составляет около 1 см в столетие.
Вековые смещения в положении геоцентра можно объяснить такими причинами:
- изменением уровня моря;
- изменениями в ледяном щите (в Гренландии, Антарктиде);
- тектоническими смещениями в земной коре (постледниковая отдача, движение тектонических плит, субдукции и др.).
Годовые колебания в положении геоцентра имеют амплитуда около 4 мм по координатам X, Y и порядка 10 мм по Z.
Также выявлены колебания с периодом 140, 60-70, 20 и 14 суток с амплитудами несколько миллиметров и с погрешностями амплитуд почти такого же порядка.
Движение отсчетной основы наземной сети относительно геоцентра поддается выявлению, но величина его небольшая. Учитывать изменения положения геоцентра в результатах измерений соответствующими комитетами пока не рекомендуется.
[править] Оси эллипсоида
В земных геоцентрических системах координат началом является центр масс Земли, а направление осей связывается с положением полюса Земли, ее экватора и нулевого меридиана.
Полюсом называется точка пересечения оси вращения с поверхностью. Под действием множества факторов мгновенные полюса перемещаются. В геодезических системах координат используются условные географические полюса, полученные усреднением наблюдений в разветвленных наземных сетях.
В начале прошлого столетия за определение условного полюса отвечала Международная служба широты (МСШ), в настоящее время мониторингом мгновенного смещения полюсов относительной условных занимается Международная служба вращения Земли и референцных систем (IERS) с помощью разветвленной сети из 50 с лишним станций. Эта же организация контролирует смещение центра масс Земли и прочих параметров.
Выявленный тренд движения полюсов Земли - около 1 градуса в 1 млн. лет.
В мелком масштабе времени движение обусловлено приливами земной поверхности под действием Луны и Солнца. Воздействие гравитации этих небесных тел приводит к сжатию и разжатию поверхности примерно на 1 метр.
Из за наклона плоскости экватора относительно плоскости орбиты Земли Солнце с разной силой притягивает северную и южную части планеты, что вызывает прецессию земной оси. Эффект усиливается резонансом, вызванным гравитационным взаимодействием с Луной. В результате полюса Земли каждый год смещаются на несколько метров.
Положение магнитного и географического полюса отличаются существенно. Например, в последние годы северный магнитный полюс изменяет своё положение со скоростью около 70 км в год. Поэтому, компас показывает направление на север лишь примерно.
[править] Параметры эллипсоида
Геоид - фигура сложной формы, образованная поверхностью уровня вод Мирового океана, продолженной под материками. Эта поверхность во всех точках перпендикулярна (нормальна) вектору силы тяжести, при этом эта нормаль, как правило, не проходит через центр тяжести планеты.
Эллипсо́ид — поверхность, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
Предположим, что мы выбрали некоторый эллипсоид как аппроксимацию земного геоида. При этом эллипсоид сплющивает лишь по одной оси, тем самым он остается телом вращения.
Эллипсо́ид враще́ния (сферо́ид) — это фигура, образованная при вращении эллипса вокруг одной из его осей.
СК-42 и т.п. основаны на эллипсоиде Красовского (1940), WGS-84 - на эллипсоиде GRS80.
| Эллипсоид | Использование | Большая полуось, a, м | Малая полуось, b, м | Сжатие f = (a-b)/a |
|---|---|---|---|---|
| Красовского (1940) | Россия и др.; Пулково-1942 | 6378245 | 6356863 | 1/298,3 |
| GRS80 | международный; WGS84 | 6378137 | 6356752,31425 | 1/298,25722356 |
Референц-эллипсоид Общеземной эллипсоид
[править] Топоцентрические и геоцентрические геодезические системы координат
Геодезические системы координат можно разделить на геоцентрические (общеземные, глобальные) и топоцентрические (национальные).
Глобальные системы координат минимизируют разницу между геоидом и эллипсоидом по всей поверхности Земли или большей её части, при этом:
- объем эллипсоида предполагается равным объему геоида;
- большая полуось эллипсоида лежит в плоскости экватора геоида;
- малая полуось направлена по оси вращения Земли.
Примеры систем - ПЗ-90, WGS-84.
В топоцентрической (национальной) эллипсоид располагают так, чтобы для заданной территории среднеквадратичное отклонение поверхности эллипсоида от поверхности геоида было минимальным. Отклонения на другой стороне Земли при этом может быть сколь угодно велико. Центр референц-эллипсоида может оказаться значительно смещенным от центра масс Земли. Примеры национальных систем - СК-42, СК-95.
[править] Картографические проекции
[править] Геоцентрическая инерциальная система координат
Для обеспечения работоспособности СРНС необходимо производить расчет и прогноз положения навигационных аппаратов. Их движение, в первом приближении, описывается уравнениями Ньютоновской механики, которые справедливы в инерциальной системе координат.
Любая система координат, которая жестко связана с Землей, существенно отлична от инерционной в масштабах движения космических аппаратов. Примерно за сутки эта система координат успевает развернуться относительно инерционных.
Геоцентрическая инерциальная система координат  , в первом приближении, не изменяет своей ориентации относительно инерциального пространства. Плоскость
, в первом приближении, не изменяет своей ориентации относительно инерциального пространства. Плоскость 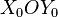 лежит в плоскости экватора Земли, ось
лежит в плоскости экватора Земли, ось 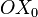 направлена в точку весеннего равноденствия - точку Весны или точку Овна
направлена в точку весеннего равноденствия - точку Весны или точку Овна  , которая лежит на линии пересечения плоскости экватора Земли и плоскости орбитального движение Земли вокруг Солнца. Ось
, которая лежит на линии пересечения плоскости экватора Земли и плоскости орбитального движение Земли вокруг Солнца. Ось 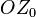 дополняет прямоугольную систему координат до правой, т.е. направлена вдоль оси вращения Земли в сторону Северного полюса.
дополняет прямоугольную систему координат до правой, т.е. направлена вдоль оси вращения Земли в сторону Северного полюса.
[править] Преобразование координат
[править] Преобразование координат прямоугольных систем
[править] Преобразование координат прямоугольных систем в геоцентрические
[править] Преобразование геодезических систем координат различных датумов
Есть различные подходы и преобразования, в основном основанные на пересчете в прямоугольные СК.
Например, СК-42 и WGS-84 связаны как (расчет на основании преобразования Молоденского):
| Направление | dX, м | dY, м | dZ, м | da, м | df, |
|---|---|---|---|---|---|
| Из СГ-42 в WGS-84 | +28.0 | -130.0 | -95.0 | -108.0 | +0.00480795 |
[править] Литература
- ГЛОНАСС. Принципы построения и функционирования / Под. ред. Перова А.И., Харисова В.Н.. — изд. 4-е, перераб. и доп.. — М.: Радиотехника, 2010. — 800 с. (подробнее...) : Глава 3, параграф 3.1
- Перов, А. И. Основы построения спутниковых радионавигационных систем. — М.: Радиотехника, 2012. — 240 с. (подробнее...) : Глава 2, параграф 2.1
[править] Замечания на будущий год
Лекция разбилась на полторы пары. Первое полупарие обсуждали:
- Понятие системы координат
- Классификация СК по различным признакам
- Понятие декартовой СК
- Локальная СК (наглядный пример - СК аэропорта)
- Локальная СК, связанная с объектом (на примере самолета)
- Углы Эйлера
- Рысканье, крен, тангаж
- Преимущества описания кватернионами
- Матрицы повротов (вывод матрицы на плоскости, обобщение на трехмерный случай).
Второе занятие (одна пара):
- Простенькая задачка на поворот осей (на 90 градусов)
- ECEF
- ECEF можно ввести множество. Нужно определиться с началом отсчета, полюсом и нулевым меридианом.
- Центр тяжести Земли и его эволюция
- Полюс и его эволюция (заодно про несовпадение с магнитным полюсом)
- Гринвич и нулевой меридиан по международному стандарту
- Человек ориентируется больше по поверхности Земли -> Геодезические СК
- Простейший вариант - аппроксимировать сферой в выбранном ECEF.
- Задачка по расчету координат на необитаемом острове
- Сфера не лучшая аппроксимация, Земля всё-таки сплюснута на 20+20 км по полюсам. Отсюда эллипсоидальные геодезические СК.
- Эллипсы бывают разные. Некоторые общеземные (тот, что в WGS), некоторые - местячковые (Красовского).
- Формулы связи ECEF и ENU.
- Следующий уровень аппроксимации - геоид. Особенно востребован у моряков.
- Датум как совокупность. Примеры датумов. Датум, как система, определяемая совокупностью станций наблюдения и математических моделей. Отсюда - расхождение их как функция времени.
- Определились с координатами на сфере. Замечательно. Но пользуемся-то мы плоскими картами. Сферический планшетов нет у нас. Отсюда - картографическая проекция.
- Классификация картографических проекций и их примеры.
- Проекция Меркатора на примере Яндекса. Минус - несохранение масштаба. Плюс - простота проверки курса.
- Первая и вторая геодезические задачи. Решение второй геодезической задачи в сферической проекции Меркатора на примере Яндекса. Предельные случаи.