11.11.2015 Взять и поделить или деление по модулю
Korogodin (обсуждение | вклад) |
Korogodin (обсуждение | вклад) |
||
| Строка 91: | Строка 91: | ||
</source> | </source> | ||
| − | возвращает ''остаток от деления'' в виде числа с плавающей точкой (numer - tquot * denom), где tquot - результат округления в сторону нуля дроби numer/denom. Иначе говоря, функция использует truncated division. | + | возвращает ''остаток от деления'' в виде числа с плавающей точкой (numer - tquot * denom), где tquot - результат округления в сторону нуля дроби numer/denom. Иначе говоря, функция использует truncated division или функцию fix(). |
{{Hider|title = fmod() (доступны fig) | {{Hider|title = fmod() (доступны fig) | ||
| Строка 101: | Строка 101: | ||
== Функция remainder == | == Функция remainder == | ||
| + | Функция<ref>remainder</ref>: | ||
| + | <source lang="C"> | ||
| + | double remainder (double numer , double denom); | ||
| + | float remainderf (float numer , float denom); | ||
| + | long double remainderl (long double numer, long double denom); | ||
| + | </source> | ||
| + | аналогична fmod(), но использует округление к ближайшему целому, то есть функцию '''round''' вместо fix. | ||
== Ссылки == | == Ссылки == | ||
<references/> | <references/> | ||
Версия 14:57, 12 ноября 2015
|
Есть некоторая неуверенность в результатах работы функций взятия модуля, для борьбы с которой составлена эта памятка.
Лично я привык к работе функции mod(a, b) в MATLAB, которая приводит a к диапазону [0 b] или [b 0] (в зависимости от знака b) путем прибавления/вычитания целого числа b к/из a. Что выражается в формуле:
- mod(a, b) = a - floor(a ./ b)*b,
где функция floor - округление в сторону минус бесконечности.
Операция взятия остатка по модулю замечательна своими свойствами:
- (a+b)mod n = [a(mod n) + b(mod n)]mod n
- (a-b)mod n = [a(mod n) - b(mod n)]mod n
- (a*b)mod n = [a(mod n) * b(mod n)]mod n
- [c*(a+b)]mod n = [c*a(mod n) + c*b(mod n)]mod n
Как оказалось, делить можно по-разному, в зависимости от функции, которую мы используем для округления[1]. Для себя я теперь разделяю понятия остатка от деления (remainder after devision) и приведения числа по модулю (modulus after devision). Первое - результат школьного деления столбиком, где остатку приписывается знак согласно принятому соглашению. В этом случае для округления используется fix() - truncated division. Второе - приведение числа к диапазону, использует floor() - floored division. Результаты будут отличаться тогда, когда аргументы имеют разный знак.
Так какие функции и операторы реализуют остаток от деления, какие взятие по модулю, и как они зависят от типов аргументов? Ниже представлены результаты, полученные на Oryx 161, компилятор из Xilinx SDK 2014.4 ( gcc version 4.8.3 20140320 (prerelease) (Sourcery CodeBench Lite 2014.05-23)).
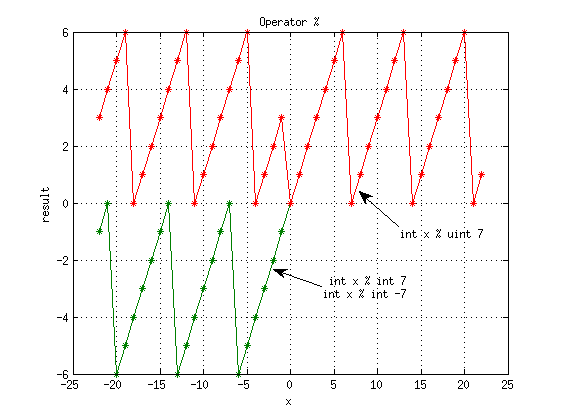
Оператор %
(int(13)) % (int(-7)) = 6
(int(13)) % (int(-5)) = 3
(int(13)) % (int(-1)) = 0
(int(13)) % (int(1)) = 0
(int(13)) % (int(5)) = 3
(int(13)) % (int(7)) = 6
(int(13)) % (int(17)) = 13
(int(-13)) % (int(-17)) = -13
(int(-13)) % (int(-7)) = -6
(int(-13)) % (int(-5)) = -3
(int(-13)) % (int(-1)) = 0
(int(-13)) % (int(1)) = 0
(int(-13)) % (int(5)) = -3
(int(-13)) % (int(7)) = -6
(int(-13)) % (int(17)) = -13
(unsigned int(13)) % (int(-17)) = 13
(unsigned int(13)) % (int(-7)) = 13
(unsigned int(13)) % (int(-5)) = 13
(unsigned int(13)) % (int(-1)) = 13
(unsigned int(13)) % (int(1)) = 0
(unsigned int(13)) % (int(5)) = 3
(unsigned int(13)) % (int(7)) = 6
(unsigned int(13)) % (int(17)) = 13
(int(13)) % (unsigned int(1)) = 0
(int(13)) % (unsigned int(5)) = 3
(int(13)) % (unsigned int(7)) = 6
(int(13)) % (unsigned int(17)) = 13
(int(-13)) % (unsigned int(1)) = 0
(int(-13)) % (unsigned int(5)) = 3
(int(-13)) % (unsigned int(7)) = 5
(int(-13)) % (unsigned int(17)) = 5
(unsigned int(13)) % (unsigned int(1)) = 0
(unsigned int(13)) % (unsigned int(5)) = 3
(unsigned int(13)) % (unsigned int(7)) = 6
(unsigned int(13)) % (unsigned int(17)) = 13
Следует обратить внимание:
- int a % uint b = mod(*(uint*(&a)), b) - результаты для -13%(int 7) и -13%(uint 7) различаются; если брать int % uint, то int интерпретируется как uint, например, -1 превращается в 2^32-1.
- uint a % int b = b<0 ? a : mod(a, b) - взятие uint % отрицательного числа - холостая операция, результат - исходный uint
- int a % int b = sign(a) * mod(|a|, |b|) - как подсказывает стандарт, до C (ISO 1999) и C++ (ISO 2011) знак зависел от реализации, теперь же применяется знак делимого
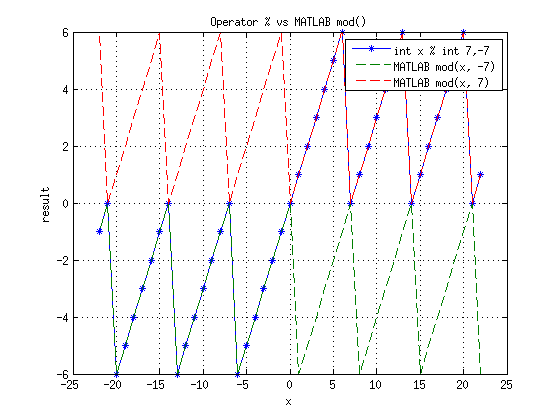
- int a % int b = (MATLAB)rem(a, b) - ведет себя как функция rem() в MATLAB: rem(a, b) = a - fix(a/b)*b, где fix() - функция округления в сторону нуля
- int a % int b ведет себя как функция mod() в MATLAB только при совпадении знаков аргументов, иначе есть смещение на b (за исключением точек, в которых результат ноль)
Выводы:
- Оператор % дает в нашей системе остаток от деления (truncated division)
Для наглядности построены графики (доступен fig):
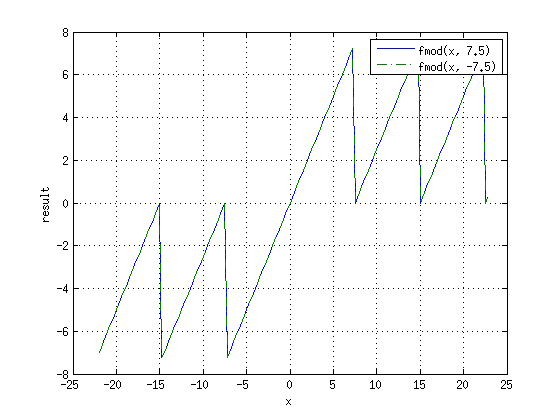
Функция fmod
Функция[2]:
возвращает остаток от деления в виде числа с плавающей точкой (numer - tquot * denom), где tquot - результат округления в сторону нуля дроби numer/denom. Иначе говоря, функция использует truncated division или функцию fix().
Функция remainder
Функция[3]:
float remainderf (float numer , float denom);
long double remainderl (long double numer, long double denom);
аналогична fmod(), но использует округление к ближайшему целому, то есть функцию round вместо fix.
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.