11.11.2015 Взять и поделить или деление по модулю

Материал из SRNS
Перейти к: навигация, поиск

Содержание

Есть некоторая неуверенность в результатах работы функций взятия модуля, для борьбы с которой составлена эта памятка.

Лично я привык к работе функции mod(a, b) в MATLAB, которая приводит a к диапазону [0 b] или [b 0] (в зависимости от знака b) путем прибавления/вычитания целого числа b к/из a. Что выражается в формуле:

mod(a, b) = a - floor(a ./ b)*b,

где функция floor - округление в сторону минус бесконечности.

Операция взятия остатка по модулю замечательна своими свойствами:

(a+b)mod n = [a(mod n) + b(mod n)]mod n
(a-b)mod n = [a(mod n) - b(mod n)]mod n
(a*b)mod n = [a(mod n) * b(mod n)]mod n
[c*(a+b)]mod n = [c*a(mod n) + c*b(mod n)]mod n

Как оказалось, делить можно по-разному, в зависимости от функции, которую мы используем для округления[1]:

  • truncated division modulo - используется функция fix() - округление в сторону нуля, в результате имеем остаток от деления абсолютных значений аргументов, знак используем от первого.
  • floored division modulo - используется функция floor() - округление в сторону минус бесконечности, в результате приводим число к интервалу [0 b] для положительных b или [b 0] для отрицательных.
  • и т.д.

Для себя я теперь разделяю понятия остатка от деления (remainder after devision) и приведения числа по модулю (modulus after devision) соответственно.

Как показало исследование ниже, результаты будут отличаться тогда, когда аргументы имеют разный знак.

Так какие функции и операторы реализуют остаток от деления, какие взятие по модулю, и как они зависят от типов аргументов? Ниже представлены результаты, полученные на Oryx 161, компилятор из Xilinx SDK 2014.4 ( gcc version 4.8.3 20140320 (prerelease) (Sourcery CodeBench Lite 2014.05-23)).


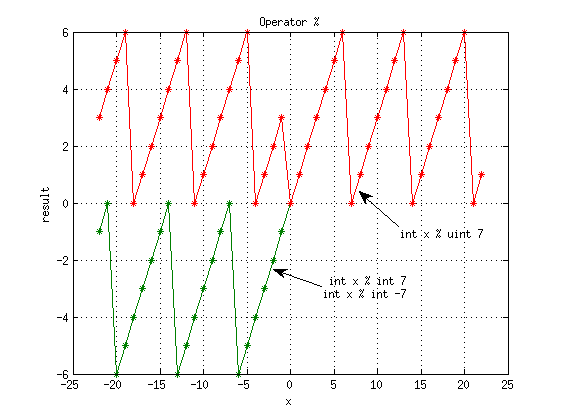
Оператор %


Следует обратить внимание:

  • int a % uint b = mod(*(uint*(&a)), b) - результаты для -13%(int 7) и -13%(uint 7) различаются; если брать int % uint, то int интерпретируется как uint, например, -1 превращается в 2^32-1.
  • uint a % int b = b<0 ? a : mod(a, b) - взятие uint % отрицательного числа - холостая операция, результат - исходный uint
  • int a % int b = sign(a) * mod(|a|, |b|) - как подсказывает стандарт, до C (ISO 1999) и C++ (ISO 2011) знак зависел от реализации, теперь же применяется знак делимого
  • int a % int b = (MATLAB)rem(a, b) - ведет себя как функция rem() в MATLAB: rem(a, b) = a - fix(a/b)*b, где fix() - функция округления в сторону нуля
  • int a % int b ведет себя как функция mod() в MATLAB только при совпадении знаков аргументов, иначе есть смещение на b (за исключением точек, в которых результат ноль)

Выводы:

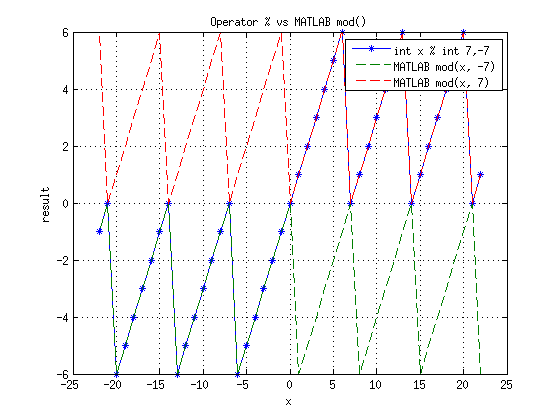
  • Оператор % дает в нашей системе остаток от деления (truncated division modulo)
  • Функция mod() в MATLAB производит floored modulo, функция rem() в MATLAB - truncated modulo.

Для наглядности построены графики (доступен fig):


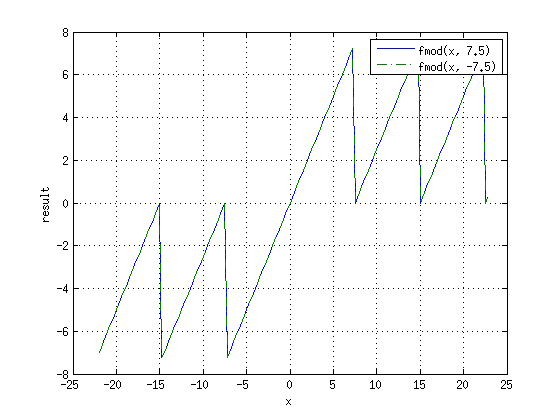
Функция fmod

Функция[2]:

double fmod (double numer, double denom)

возвращает остаток от деления в виде числа с плавающей точкой (numer - tquot * denom), где tquot - результат округления в сторону нуля дроби numer/denom. Иначе говоря, функция использует truncated division или функцию fix(). От знака второго аргумента результат не зависит. Буква f в названии функции - отсылка к float, а не floored!


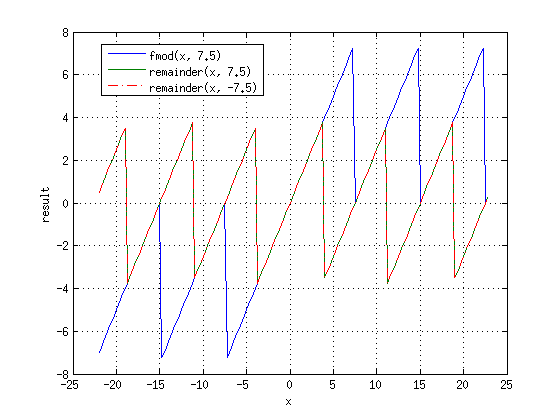
Функция remainder

Функция[3]:

     double remainder  (double numer     , double denom);
      float remainderf (float numer      , float denom);
long double remainderl (long double numer, long double denom);

аналогична fmod(), но использует округление к ближайшему целому, то есть функцию round вместо fix. От знака второго аргумента результат не зависит.


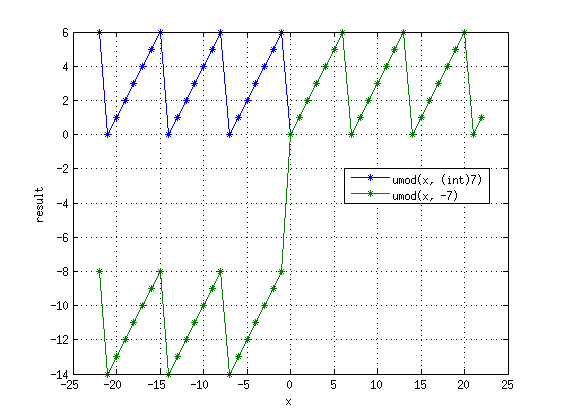
Макрос umod

Для имитации matlab'овского mod() для целых чисел у нас существует макрос umod:

#define umod(x, y)  ( ((x)>=0) ? ((x)%(y)) : ((((x)+1)%(y))+(y)-1) )

При положительных y она работает как и ожидается - реализует floored modulo, при отрицательных есть проблемы.


Кроме того, если в неё мешать использование uint и int, то можно получить интересные эффекты, описанные выше.


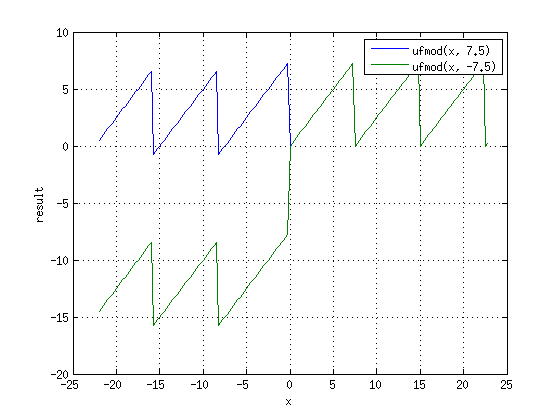
Макрос ufmod

Аналогичен umod, но использовался для чисел типа double. Вызывал ошибки, поэтому сейчас не используется.

#define ufmod(x, y) ( ((x)>=0) ? (fmod((x), (y))) : (fmod(((x)+1),(y))+(y)-1) )

Графики показывают, что макрос дает ошибочные значения для отрицательных чисел.


Кроме того, если в неё мешать использование uint и int, то можно получить интересные эффекты, описанные выше.

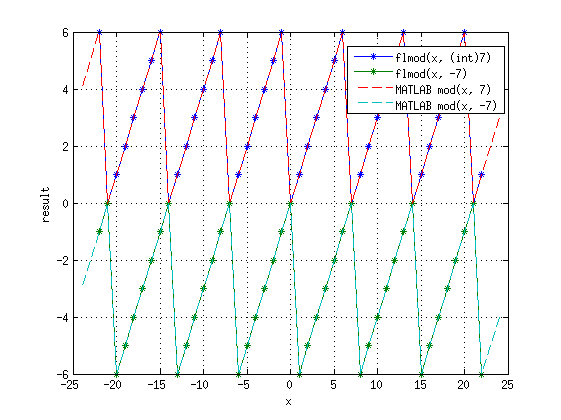
Функция flmod(int, int)

Для исправления недостатков макроса umod создана функция flmod(int, int):

int flmod(int x, int y) {
    if (y >= 0)
        return ( (x>=0) ? (x%y) : (((x+1)%(y))+(y)-1) );
    else
        return -( (x<=0) ? (-x%-y) : (((-x+1)%(-y))+(-y)-1) );
}

Результаты её выполнения совпадают с MATLAB mod(), она реализует floored modulo:


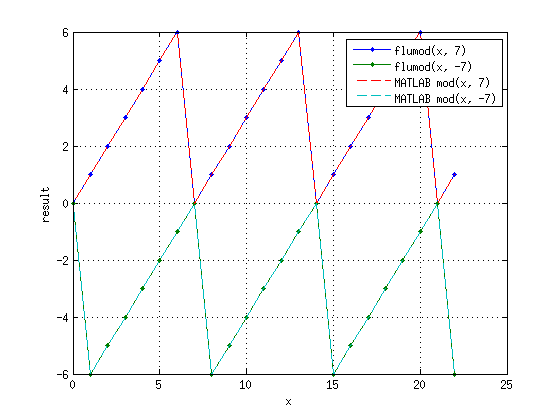
Функция flumod(unsigned int, int)

Функция возвращает floored modulo для пары (unsigned int, int)


Результаты её выполнения совпадают с MATLAB mod():


Результаты тестов на большие входные значения:


Функция flmod2POW32(int)

Функция возвращает floored modulo для пары (2^32, int)


Результаты тестов (совпадают с octave):


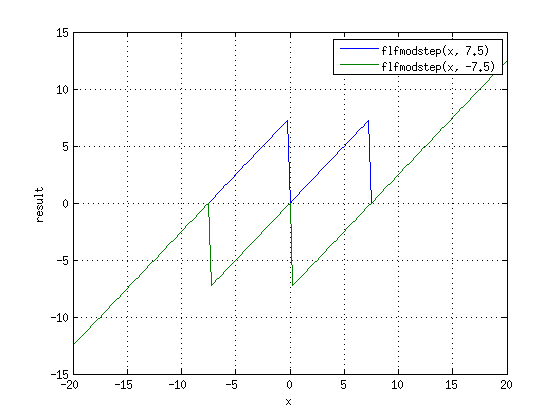
Функция flfmodstep(double, double)

При переполнениях возникает задача сделать один шаг операции floored mod, прибавить или удалить только один base


Симуляция переполнения знакового регистра

Пусть есть регистр, значение которого интерпретируется как число в доп.коде. Тогда переполнение регистра можно имитировать в MATLAB'е преобразованием:

% N - число разрядов регистра
% x - число, которое пытаемся записать в регистр
% y - число, которое окажется в регистре
y = mod(x + 2^(N-1), 2^N) - 2^(N-1);


Ссылки

  1. ↑ Wiki: Modulo operation
  2. ↑ http://www.cplusplus.com/reference/cmath/fmod/
  3. ↑ http://www.cplusplus.com/reference/cmath/remainder/

— Корогодин Илья • 18:40, 11 ноября 2015 • нет комментариев

[ Хронологический вид ]Комментарии

(нет элементов)

Войдите, чтобы комментировать.

Источник — «https://2fwww.srns.ru/index.php?title=Blog:Korogodin/11.11.2015_Взять_и_поделить_или_деление_по_модулю&oldid=16311»
Персональные инструменты
Пространства имён

Варианты
Действия
SRNS Wiki
Рабочие журналы
Приватный файлсервер
QNAP Сервер
Инструменты