Псевдодальность, псевдоскорость, псевдофаза (ОП СРНС, лекция)

Понятие псевдодальности

Рассмотрим некоторую ECI СК, в которой находится навигационный спутник и приемник. Спутник излучает непрерывный сигнал, причем сигнал имеет специальную структуру, позволяющую каждому моменту сигнала сопоставить число. Таким образом, сигнал в каждой точке пространства задает шкалу времени - сигнальное время [ссылка на Харисова]. Так как сигнал формируется навигационным спутником от его бортового стандарта частоты, то сигнальное время в момент излучения, в первом приближении, совпадает с бортовой шкалой времени спутника.

Сигнал от спутника распространяется в пространстве, точки с одинаковым сигнальным временем образуют эквивременные поверхности. Для свободного пространства в дальней зоне эти поверхности - сферы. Центр сферы - то место, где находился спутник в сигнальное время. Радиус сферы нарастает, увеличиваясь со скоростью распространения сигнала в пространстве (эта скорость может быть как групповой, так и фазовой скоростью сигнала, в зависимости от носителя шкалы времени в сигнале).

Опыт первого года

Начал занятие с простеньких задачек на предыдущую тему:

1. Над каким городом нашей страны сейчас находится солнце в зените. Время было 14:00. По UTC0 - 10:00. За два часа Земля повернется на 30 градусов. 30 градусов восточной долготы - примерно Питер. Заодно вспомнили про существование декретного и летнего времени, сдвига наших часов от UTC0.
2. Над каким городом реальный зенит, когда в Москве часы показывают полдень. Смещение еще 30 градусов. Итого 60. Это долгота Екатеринбурга. Шокирующая правда - полдень в Москве далеко не полдень. А теперь следовало бы ещё учесть уравнение времени, внести поправку до 15 минут.
3. Можно развить мысль (в этом году так не делал) - во сколько по московским часам у нас зенит солнца. А с учетом уравнения времени?

Далее я попросил дать определение UTC, но это требует напоминания всей предыдущей лекции. Вопрос не удачен. Зато показывает, что можно ещё раз повторять лекцию - осадок знаний остался не очень-то большой.

Далее я начал определять псевдодальность. Ввел ECI, в ECI спутник и приемник. При каждом - своя шкала времени. Сигнал, который излучает приемник, является шкалой времени. Хотя бы чисто по определению. Мы можем каждому событию - точке сигнала - сопоставлять некоторое значение времени. Точно так же, как у нас колебание опорного генератора задает шкалу времени приемника или спутника. Назовем это время сигнальным. Причем, если присмотреться, то можно за основу взять функцию фазы несущей. А можно - фазы огибающей, модуляции. Соответственно, один и тот же сигнал может задавать несколько сигнальных шкал времени. Первое пусть будет фазовым сигнальным временем, второе - кодовым. Идея: Тут стоит сделать пояснительную картинку. График абсолютное время-фаза (огибающей или несущей). Ниже пририсовать осциллограмму сигнала, по-точкам сопоставить сигнал, фазовое и кодовое время. Нужно больше иллюстраций сигнального времени. Тут, кстати, возникает тонкий момент. Модулирующая функция может быть дискретной. Тогда и время там меняется дискретно. А вот в кусочках между дискретами мы аппроксимируем имеющийся у нас шкалой времени (ШВП).

Сигнал формируется из ботовой шкалы времени. Кстати, на прошлом занятии нужно повторить несколько раз определение БШВ, СШВ, ШВП. Чтобы въелось. Сигнальное время формируемого сигнала повторяет бортовое время. Далее этот сигнал начинает распространяться в пространстве. Соответствующие картинки. Точка у спутника - осциллограммка сигнала. Рассмотрим некоторое направление, точку на нём. Пусть отстоит на R от точки излучения. Тогда осциллограммка там - смещенная на R/c. Чему равно сигнальное время там в точке R/c? Тому самому сигнальному времени в момент излучения. Такие точки во всех направлениях от спутника образуют поверхность - сферу - с одинаковым сигнальным временем. Временем излучения со спутника, который в тот самый момент находился в центре этой сферы. Эта точка сигнала излучилась, спутник улетел, и чем больше проходит время - тем шире расползается сфера с одинаковым сигнальным временем. Если нарисовать график расстояние-время, то мы получим хорошо знакомый световой конус из СТО (наверное, не стоит обременять их головы лишними мыслями). Идея: Круто было бы сделать анимацию, как в англовики про эффект Доплера. Летящий спутник и расходящиеся эквисигнальные сферы.

Проходят миллисекунды, и эта сфера добирается до приемника. Приемник принимает сигнал. Делает он это непрерывно. Но вот решение формирует дискретно. Наступает время очередных измерений, по шкале времени приемника это 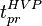$t_{pr}^{HVP}$. Сигнальное время сигнала в этот самый момент времени - время излучения этой точки огибающей/несущей сигнала в бортовой шкале времени $t_{izl}^{BHV}$.

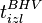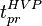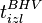Псевдозадержка, по определению, разница $t_{pr}^{HVP}$ и $t_{izl}^{BHV}$. Псевдодальность - псевдозадержка, умноженная на скорость света.

О решении навигационной задачи на основе псевдодальностей и информации о положении спутника. Требования к сигналу - возможность легко и точно восстановить по нему сигнальное время + возможность получить эфемериды и т.п. информацию. Система уравнений. Как её решать. Итеративный метод.

Псевдофаза. Схожее понятие, но теперь идет сравнение фаз сигналов принятого и опорного, что эквивалентно вычитанию фазового сигнального времени. Специфика - неоднозначность. Ну и единицы измерения - градусы, радианы, циклы. Но это мелочи, в чём именно считать. В итоге возникает величина почти соответствующая псевдодальности, обладающая значительно меньшей шумовой ошибкой, но при этом неоднозначностью. Картинка с неоднозначностью и погрешностями. Длина волны. Есть методы, позволяющие узнать число лишних 2 пи. На основе сравнения с псевдодальностью и избыточности. Когда спутников четыре - есть множество допустимых комбинаций. Когда увеличиваем число спутников - часть комбинаций отпадает. Поэтому ГЛОНАСС в гражданских приемниках в 90-х годах использовался только в геодезии и т.п. - проще было разрешать фазовую неоднозначность.

Псевдочастота. Производная по времени. Вопрос - какому времени? Обычно берут по ШВП. О эффекте Доплера. Пересчет в псевдоскорости. Можно решить аналогичную задачу. Метод псевдоскоростной метод. При взятии производной постоянный 2пиN исчезает. Проблемы нет. Реализуется с помощью ЧАП.

DOP и его разновидности. Картинки. Наглядная демонстрация.