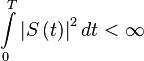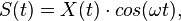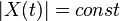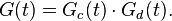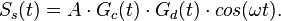Требования, предъявляемые к навигационным сигналам (ОП СРНС, лекция)

Навигационные определения формируются в СРНС второго поколения на базе псевдодальномерного метода. Навигационный сигнал должен позволять реализовывать этот метод.

Что есть сигнал? Можно ввести множество определений, но одно из самых элегантных: сигнал - функция с конечной энергией:

$\int \limits^T_0 \left| S \left( t \right) \right|^2 dt < \infty$

Под это определение попадает множество самых разнообразных функций. Но не все они подходят на роль навигационного радиосигнала. Давайте поставим себя на место разработчика навигационной системы. Сигнал какой структуры выбрать? Какие требования к нему предъявить?

На качественном уровне, укрупнено, сигнал каждого НС должен:

• Позволять хорошо определять псевдодальность;
• Передавать информацию о положении НС системы;
• Быть отличимым от сигналов других НС;
• Не мешать другим радиосистемам;
• Не требовать для приема и передачи сложной аппаратуры.

Радиосигналы в общем виде могут быть представлены в виде произведения низкочастотного комплексного сигнала и несущей:

$S(t) = Re \left[ X(t) \cdot exp(j\omega t) \right]$.

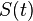Если $S(t)$ - вещественный сигнал со спектром, симметричным относительно несущей, то выражение упрощается:

$S(t) = X(t) \cdot cos(\omega t),$

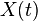где $X(t)$ - вещественный низкочастотный сигнал, спектр которого должен быть значительно уже несущей частоты.

Такие сигналы и используются в СРНС второго поколения. Отличаются они несущими частотами и видом функции 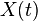$X(t)$.

Формально стоит разделять сигнал излучаемый со спутника 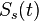$S_s(t)$ и принимаемый НАП 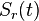$S_r(t)$. Вид второго определяется первым, но он имеет дополнительную задержку, фазовый сдвиг и существенно ослаблен. Важно выбрать параметры сигнала 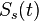$S_s(t)$ так, чтобы сигнал 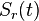$S_r(t)$ позволял решать навигационную задачу. Тут нужна картинка с линией распространения.

Минимизация пик-фактора

Пик-фактор - отношение максимального (пикового) значения напряжения к среднеквадратическому.

Минимальным пик-фактором обладают сигналы с постоянной огибающей - сигналы, для которых модуль вещественного низкочастотного сигнала неизменен:

$\left| X(t) \right| = const$

Таким образом, функция 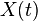$X(t)$ может быть представлена в виде

$X(t) = A \cdot G(t),$

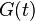где $G(t)$ принимает значения -1, 1.

Функция 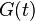$G(t)$ задает фазовую двухуровневую манипуляцию. В общем случае, она может быть представлена в виде перемножения функции манипуляции дальномерным кодом 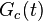$G_c(t)$ и функции манипуляции данными $G_d(t)$:

$G(t) = G_c(t) \cdot G_d(t).$

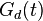Тогда вид излучаемого сигнала в общем случае:

$S_s(t) = A \cdot G_c(t) \cdot G_d(t) \cdot cos(\omega t).$

Выбор несущей частоты

В спутниковых радионавигационных системах второго поколения используются несущие частоты L-диапазона - от 1.1 до 1.6 ГГц. С одной стороны, данные частоты выделены соответствующими международными комитетами. С другой - они являются хорошим компромиссом между сложностью аппаратуры, затуханием при распространении и габаритами антенны.

Ограничение мощности

Мощность, доступная для излучения с искусственного спутника Земли, ограничена. Самые крупные и сложные коммерческие спутники связи обеспечивают питание полезной нагрузки мощностью до 14 кВт. Но эти аппараты имеют размах солнечных батарей порядка 40 метров и массу до 7 тонн. Навигационные же спутники, ввиду их массовости, должны быть значительно проще. Кроме того, энергия нужна не только на излучение навигационных сигналов, но и на телеметрию, межспутниковые измерения, работу бортового комплекса и т.д. Да и число навигационных сигналов, излучаемых с борта одного спутника, может приближаться к десяти. В итоге разумная излучаемая мощность одного сигнала - десятки Ватт.

Мощность сигнала, принимаемого потребителем, определяет требования к модуляции и структуре сигнала. Рассчитаем её.

Типовой расчет мощности сигнала (ГЛОНАСС или Основы, можно у доски)

Предоставление эфемеридных данных и альманаха

Для передачи эфемеридной информации можно использовать и другие каналы связи, но удобнее - совмещать в навигационном сигнале функции носителя сигнального времени и навигационных данных.

BER

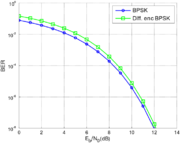
Наибольшей помехоустойчивостью обладают сигналы с модуляцией ФМ-2 и ФМ-4. Оценим скорость, с которой можно передавать навигационное сообщение при расчетном уровне мощности сигнала.

В навигационном сообщении необходимо передать информацию о состоянии спутников, информацию для краткосрочного и долгосрочного расчета их положения. Итого сообщение набирает около несколько тысяч бит. Так, суперкадр в ГЛОНАСС - 7500 бит, полное сообщение в GPS - 37500 бит.

Точность определения псевдодальности

Сигнал должен позволять точно восстанавливать кодовое сигнальное время несмотря на действие шумов.

Кодовое сигнальное время определяется по огибающей сигнала - модуляции несущей частоты.

Допустим, используется некоторый сигнал 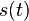$s(t)$. Допустим, на приемной стороне известна его частота, амплитуда, начальная фаза - то есть все параметры, кроме задержки огибающей. Рассмотрим случай, когда сигнал наблюдается на фоне белых некоррелированных гауссовых шумов 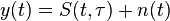$y(t) = S(t, \tau) + n(t)$ на некотором временном интервале длительностью 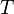$T$. Считается, что задержка на этом интервале не меняется. В статистической теории радиотехнических систем найдена потенциальная граница точности (СКО) оценки задержки 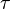$\tau$ такого сигнала по наблюдениями $y(t)$:

$\sigma_{\tau} = \frac{1}{\sqrt{2q}\beta}$,

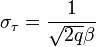где

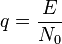$q = \frac{E}{N_0}$ - отношение сигнал/шум,

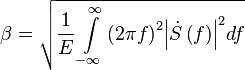$\beta = \sqrt{{\frac{1}{E}\int\limits_{ - \infty }^\infty {{{\left( {2\pi f} \right)}^2}{{\left| {\dot S\left( f \right)} \right|}^2}df} }}$ - эффективная ширина спектра радиосигнала,

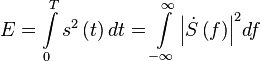$E = \int\limits_0^T {{s^2}\left( t \right)dt} = \int\limits_{ - \infty }^\infty {{{\left| {\dot S\left( f \right)} \right|}^2}df}$ - энергия сигнала за время наблюдения,

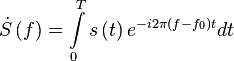$\dot S\left( f \right) = \int\limits_0^T {s\left( t \right){e^{ - i2\pi (f-f_0)t}}dt}$ - спектральная плотность сигнала записанная относительно несущей.

В реальной аппаратуре полоса радиотракта ограничена, поэтому интеграл при расчете следует ограничить в пределах. Кроме того, эта постановка задачи не в полной мере отражает работу приемника - задержка меняется во времени, поэтому используют системы слежения. Тем не менее, эти выражения позволяют установить качественно связь между параметрами сигнала и точностью оценки его задержки (а значит и кодового сигнального времени, псевдозадержки, псевдодальности).

В формуле эффективной ширины спектра присутствует множитель вида 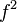$f^2$ - парабола. Следует вывод - по гармоническому колебанию задержку не определить, а для уменьшения ошибки определения задержки следует увеличивать ширину спектра сигнала. В пределе наилучшую точность обеспечивают сигнал с двумя компонентами в спектре, максимально отдаленными от несущей.

Точность определения псевдоскорости

Аналогичные выражения можно найти для потенциальной точности оценки доплеровского смещения частоты:

$\sigma_{\tau} = \frac{1}{\sqrt{2q}\alpha}$,

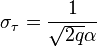где

$\alpha = \sqrt{{\frac{1}{E}\int\limits_0^T {{{\left( {2\pi t} \right)}^2}} {s^2}\left( t \right)dt} }$ - эффективная длительность сигнала.

Передающая аппаратура работает эффективно при использовании сигналов с постоянной огибающей, а для них:

$\alpha = \sqrt{ {\frac{2}{T}\int\limits_0^T {{{\left( {2\pi t} \right)}^2}} {{\cos }^2}\left( {\omega t} \right)dt} } \approx 3,628T$,

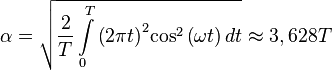откуда можно сделать вывод, что их конкретный вид не влияет на точность определения доплеровского сдвига, а значит и псевдоскорости.

Возможность разделения каналов

TDMA не удобен, остается CDMA и FDMA.

Время поиска сигнала

При включении навигационного приемника сначала решается задача по-иска сигналов, которая заключается в формировании грубых оценки задержки и доплеровского смещения частоты сигналов, находящихся в зоне радиовидимости.

Устойчивость к многолучевому распространению

Определяется корреляционными свойствами сигнала, точнее кода. Огибающая многолучевости.

Помехоустойчивость приема сигнала

Спектральное разделение помехи и сигнала.

Внутрисистемные помехи

Вариация - опять же спектральное разделение.

Опыт

Первую половину пары обсуждали результаты обработки данных с лабораторной работы. Типичные вопросы:

• Что за таблички? Что за наборы чисел, что они обозначают?
• Каким образом получено навигационное решение?
• Сколько решений было получено? За сколько итераций?
• Что будет, если введем другие разности между псевдодальностью и дальностью?
• Проверка результатов решения задачи прямым измерением. Точность выписываю на титульник.
• Задачка на DOP. Погрешности по разным координатам разные. Как изменятся погрешности по OX и по OY, если поменяем положение одного из НС?

Впечатления от ответов на вопросы на титульник.

Вторая половина пары - требования к навигационным сигналам.

Определение сигнала как функции с конечной энергией. Давайте определимся с требованиями к нашим сигналам и с их помощью усечем множество всевозможных сигналов - оставим только те, что нам подходят.

Кратко что нам нужно от сигналов - пять пунктов, обозначенных в основном тексте.

Начинаем с требований от передающей аппаратуры. Минимизация пик-фактора (следовало бы ввести чётко это понятие). Отсюда сигналы с постоянной огибающей. Второе ограничение - мощность излучателя на уровне 20-40 Вт. Тут бы следовало произвести расчет мощности у земли

Следовало бы аккуратно ввести G(t)*cos. В принципе, это можно записать для любого узкополосного сигнала. Вот и выход - констатировать узкополосность, откуда вывести такой вид сигнала в общем случае. Далее сказать, что норма G(t) должна быть единицей для минимизации пик-фактора.

Ещё раз напомнить кодовое и фазовое сигнальное время. Первое - по задержке G(t), второе - по фазе cos'инуса. Итак, нам нужно четко измерять задержку tau: G(t-tau) несмотря на действие шумов. Задачка статистической теории. Ограничения интеграла полосой тракта. Формула для СКО. Из неё следует, что спектр G(w) надо расширять, вплоть до двух гармоник. Прикидываем порядок ширины спектра для 1с измерений с точностью 1м. Должно получиться порядка МГц.

Тут закончилась вторая половина пары.

У нас низкая мощность сигнала у земли. А данные всё ещё надо передавать. Наиболее помехоустойчивы - ФМ-2 и ФМ-4. У следящих систем есть ещё запас порядка 20-30 дБ. Поэтому нам надо получать данные при уровне сигнала -180дБВт. Отсюда максимальная битовая скорость - порядка 50 бит/с. Для передачи данных вполне подходит. Но ширина спектра такого сигнала - 100 Гц. А нам для точного измерения дальности нужны МГц.

Отсюда - спектрорасширяющая модуляция, она же дальномерный код. Специальная последовательность, известная на стороне потребителя, которая расширяет спектр сигнала и позволяет точно измерять его задержку.

Мысль: получился неправильный порядок изложения лекции. Слишком много перекрестных связей. Нет четкой причинно-следственной связи, есть многомерное пространство вариантов. От этого не уйти. Нужно начинать с того, что в навигационных системах в итоге остановились на сигналах вида S = A * G * D * cos(wt). И потом объяснять, почему именно одна несущая, почему она именно такая. Почему такая маленькая амплитуда. Почему такая низкая скорость передачи сообщения. Почему потребовалась спектрорасширяющая последовательность. Зачем её делать периодичной (поиск сигнала). За счет чего реализуется разделение сигналов. Как минимизировали внутрисистемные, межсистемные помехи и внеполосное излучение. Увеличение коэффициента спектрального разделения. Антиимитационная модуляция.